题目内容
 二次函数图象的顶点在原点O,经过点A(1,
二次函数图象的顶点在原点O,经过点A(1,| 1 |
| 4 |
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.
考点:二次函数综合题
专题:代数几何综合题
分析:(1)根据题意可设函数的解析式为y=ax2,将点A代入函数解析式,求出a的值,继而可求得二次函数的解析式;
(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;
(3)首先可得∠FMH=30°,设点P的坐标为(x,
x2),根据PF=PM=FM,可得关于x的方程,求出x的值即可得出答案.
(2)过点P作PB⊥y轴于点B,利用勾股定理求出PF,表示出PM,可得PF=PM,∠PFM=∠PMF,结合平行线的性质,可得出结论;
(3)首先可得∠FMH=30°,设点P的坐标为(x,
| 1 |
| 4 |
解答:(1)解:∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1,
)代入y=ax2得:a=
,
∴二次函数的解析式为y=
x2;
 (2)证明:∵点P在抛物线y=
(2)证明:∵点P在抛物线y=
x2上,
∴可设点P的坐标为(x,
x2),
过点P作PB⊥y轴于点B,则BF=
x2-1,PB=x,
∴Rt△BPF中,
PF=
=
x2+1,
∵PM⊥直线y=-1,
∴PM=
x2+1,
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)解:当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴
x2+1=4,
解得:x=±2
,
∴
x2=
×12=3,
∴满足条件的点P的坐标为(2
,3)或(-2
,3).
∴设二次函数的解析式为y=ax2,
将点A(1,
| 1 |
| 4 |
| 1 |
| 4 |
∴二次函数的解析式为y=
| 1 |
| 4 |
 (2)证明:∵点P在抛物线y=
(2)证明:∵点P在抛物线y=| 1 |
| 4 |
∴可设点P的坐标为(x,
| 1 |
| 4 |
过点P作PB⊥y轴于点B,则BF=
| 1 |
| 4 |
∴Rt△BPF中,
PF=
(
|
| 1 |
| 4 |
∵PM⊥直线y=-1,
∴PM=
| 1 |
| 4 |
∴PF=PM,
∴∠PFM=∠PMF,
又∵PM∥y轴,
∴∠MFH=∠PMF,
∴∠PFM=∠MFH,
∴FM平分∠OFP;
(3)解:当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴
| 1 |
| 4 |
解得:x=±2
| 3 |
∴
| 1 |
| 4 |
| 1 |
| 4 |
∴满足条件的点P的坐标为(2
| 3 |
| 3 |
点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、角平分线的性质及直角三角形的性质,解答本题的关键是熟练基本知识,数形结合,将所学知识融会贯通.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
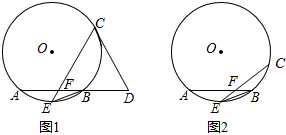 如图1,在⊙O中,E是
如图1,在⊙O中,E是
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠BCD.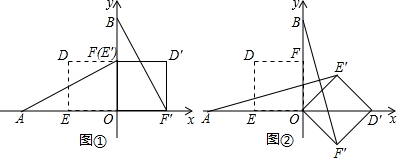
 如图,AB是⊙O的直径,C、D两点在⊙O上,且BC=CD,过点C作CE⊥AD,交AD的延长线于点E,交AB的延长线于点F.
如图,AB是⊙O的直径,C、D两点在⊙O上,且BC=CD,过点C作CE⊥AD,交AD的延长线于点E,交AB的延长线于点F. 如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.
如图,方格纸中每个小正方形的边长均为1,四边形ABCD的四个顶点都在小正方形的顶点上,点E在BC边上,且点E在小正方形的顶点上,连接AE.