题目内容
9.当0≤x≤2时,二次函数y=x2-2mx+m2+2m有最小值为3,则m的值为$\frac{3}{2}$或-3.分析 先求出二次函数的对称轴为直线x=m,然后分①m<0时,x=0函数有最小值,②0≤m≤2时,x=m函数有最小值,③m>2时,x=2函数有最小值分别列方程求解即可.
解答 解:∵y=x2-2mx+m2+2m=(x-m)2+2m,
∴二次函数的对称轴为直线x=m,
①m<0时,x=0函数有最小值,
此时,m2+2m=3,
解得m1=-3,m2=1(舍去),
②0≤m≤2时,x=m函数有最小值,
此时,2m=3,
解得m=$\frac{3}{2}$,
③m>2时,x=2函数有最小值,
此时,4-4m+m2+2m=3,
整理得,m2-2m+1=0,
解得m=1(舍去),
综上所述,m的值为$\frac{3}{2}$或-3.
故答案为:$\frac{3}{2}$或-3.
点评 本题考查了二次函数的最值问题,主要利用了二次函数增减性,难点在于根据对称轴的情况分情况讨论.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
17.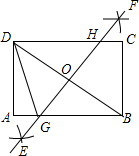 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
 如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )
如图,在矩形ABCD中,用直尺和圆规作BD的垂直平分线EF,交AB于点G,交DC于点H,若AB=4,BC=3,则AG的长为( )| A. | $\frac{25}{8}$ | B. | $\frac{7}{4}$ | C. | $\frac{7}{8}$ | D. | $\frac{5}{8}$ |
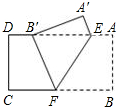 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上,的点B′处,点A落在点A′处,若AE=6,BF=10,则AB=8. 某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( )
某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( ) 已知A、B两地相距80km,甲、乙二人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DB、OC分别表示表示甲、乙二人离开A地距离S(km)与时间t(h)的函数关系,根据题中的图象填空:
已知A、B两地相距80km,甲、乙二人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DB、OC分别表示表示甲、乙二人离开A地距离S(km)与时间t(h)的函数关系,根据题中的图象填空: