题目内容
 如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?
(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长.
考点:一元一次方程的应用,数轴,两点间的距离
专题:
分析:(1)根据已知可得B点表示的数为8-14;点P表示的数为8-5t;
(2)点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC-BC=AB,列出方程求解即可;
(3)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
(2)点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据AC-BC=AB,列出方程求解即可;
(3)分①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差求出MN的长即可.
解答:解:(1)∵点A表示的数为8,B在A点左边,AB=14,
∴点B表示的数是8-14=-6,
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8-5t.
故答案为:-6,8-5t;
(2)设点P运动x秒时,在点C处追上点Q,

则AC=5x,BC=3x,
∵AC-BC=AB,
∴5x-3x=14,
解得:x=7,
∴点P运动7秒时追上点Q.
(3)线段MN的长度不发生变化,都等于7;理由如下:
∵①当点P在点A、B两点之间运动时:

MN=MP+NP=
AP+
BP=
(AP+BP)=
AB=
×14=7,
②当点P运动到点B的左侧时:
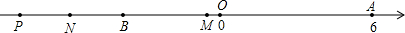
MN=MP-NP=
AP-
BP=
(AP-BP)=
AB=7,
∴线段MN的长度不发生变化,其值为7.
∴点B表示的数是8-14=-6,
∵动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
∴点P表示的数是8-5t.
故答案为:-6,8-5t;
(2)设点P运动x秒时,在点C处追上点Q,

则AC=5x,BC=3x,
∵AC-BC=AB,
∴5x-3x=14,
解得:x=7,
∴点P运动7秒时追上点Q.
(3)线段MN的长度不发生变化,都等于7;理由如下:
∵①当点P在点A、B两点之间运动时:

MN=MP+NP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②当点P运动到点B的左侧时:
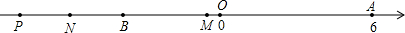
MN=MP-NP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴线段MN的长度不发生变化,其值为7.
点评:本题考查了数轴一元一次方程的应用,用到的知识点是数轴上两点之间的距离,关键是根据题意画出图形,注意分两种情况进行讨论.

练习册系列答案
相关题目
某同学本学期共参加了10次数学测试,其中90分以上有8次,该同学在这10次考试中,出现90分以上的频率是( )
| A、0.20 | B、0.80 |
| C、0.90 | D、8 |
在平行四边形ABCD中,AC与BD相交于点O,图中共有全等三角形( )
| A、1对 | B、2对 | C、3对 | D、4对 |
下列说法中,正确的是( )
| A、一组对边平行的四边形是平行四边形 |
| B、有一个角是直角的四边形是矩形 |
| C、四条边相等的四边形是菱形 |
| D、对角线互相垂直平分的四边形是正方形 |
 (1)如图,已知点C在线段AB上,线段AC=12,BC=8.点M,N分别是AC,BC的中点,求线段MN的长度;
(1)如图,已知点C在线段AB上,线段AC=12,BC=8.点M,N分别是AC,BC的中点,求线段MN的长度; 学完“判定两个直角三角形全等”后老师给学生布置了这样一道题:
学完“判定两个直角三角形全等”后老师给学生布置了这样一道题: