题目内容
8．王翰将一根粗绳对折，然后在折点处做上标记，然后再对折，再在折点处作上标记，…，依此规律，当王翰对折n次后，该粗绳上共有2n-1个标记．分析 设第n次对折粗绳上的标记数为an，根据王翰做标记的方式，列出部分an的值，根据an值的变化找出变化规律“an=2n-1”，结合该规律即可解决问题．
解答 解：设第n次对折粗绳上的标记数为an，
观察，发现规律：a1=1，a2=3，a3=7，a4=15，…，
∴an=2n-1．
故答案为：2n-1．
点评 本题考查了规律型中的数字的变化类，解题的关键是发现规律“an=2n-1”．本题属于基础题，难度不大，解决该题型题目时，罗列出部分折点的数量，根据数据的变化找出规律是关键．
练习册系列答案
相关题目
18．下列运算结果中是正数的是（ ）
| A． | （-$\frac{1}{2016}$）-1 | B． | -（$\frac{1}{2016}$）-2 | C． | -（-$\frac{1}{2016}$）0 | D． | （$\frac{1}{2016}$）-1÷（2016）-1 |
19．下列计算正确的是（ ）
| A． | 3a2-a2=3 | B． | a2•a4=a8 | C． | a8÷a2=a5 | D． | （a3）2=a6 |
16．下列计算中，正确的是（ ）
| A． | x3•x2=x4 | B． | x（x-2）=-2x+x2 | C． | （x+y）（x-y）=x2+y2 | D． | 3x3y2÷xy2=3x4 |
3．下列计算正确的是（ ）
| A． | 2x+1=2x2 | B． | x2•x3=x5 | C． | （x2）3=x5 | D． | （2x）3=2x3 |
13．为了节约资源，科学指导居民改善居住条件，小强向房管部门提出了一个购买商品房的政策性方案：
设一个3口之家购买商品房的人均面积为x平方米，缴纳房款y万元．
（1）请求出y关于x的函数关系式；
（2）若某3人之家欲购买120平方米的商品房，求其应缴纳的房款．
| 人均住房面积（平方米） | 单价（万元/平方米） |
| 不超过30（平方米）部分 | 0.4 |
| 超过30平方米部分 | 0.9 |
（1）请求出y关于x的函数关系式；
（2）若某3人之家欲购买120平方米的商品房，求其应缴纳的房款．
20．
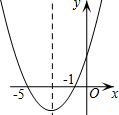如图，对于二次函数y=ax2+bx+c（a≠0）的图象，得出了下面五条信息：①c＞0；②b=6a；③b2-4ac＞0；④a+b+c＜0；⑤对于图象上的两点（-6，m ）、（1，n），有m＜n．其中正确信息的个数有（ ）
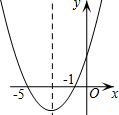如图，对于二次函数y=ax2+bx+c（a≠0）的图象，得出了下面五条信息：①c＞0；②b=6a；③b2-4ac＞0；④a+b+c＜0；⑤对于图象上的两点（-6，m ）、（1，n），有m＜n．其中正确信息的个数有（ ）| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
18．学校广播站要招聘1名记者，小亮和小丽报名参加了3项素质测试，成绩如下：
将写作能力、普通话水平、计算机水平这三项的总分由原先按3：5：2计算，变成按5：3：2计算，总分变化情况是（ ）
| 写作能力 | 普通话水平 | 计算机水平 | |
| 小亮 | 90分 | 75分 | 51分 |
| 小丽 | 60分 | 84分 | 72分 |
| A． | 小丽增加多 | B． | 小亮增加多 | ||
| C． | 两人成绩不变化 | D． | 变化情况无法确定 |