题目内容
1.(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,证明:DE=BD+CE.(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请直接写出线段DE、BD、CE之间的数量关系(不要求说明理由);
(3)将(1)中的直线m绕点A旋转,使其与BC边相交,则结论DE=BD+CE是否还成立?如成立,请你给出证明;若不成立,请写出所有可能的结论,并在图3中画出相应的图形.

分析 (1)由条件可证明△ABD≌△CAE,可得DA=CE,AE=BD,可得DE=BD+CE;
(2)由条件可知∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,可得∠DBA=∠CAE,结合条件可证明△ABD≌△CAE,同(1)可得出结论;
(3)分成m⊥BC和m与AC的夹角小于45°,大于45°三种情况进行讨论,第一种情况根据等腰三角形的性质即可判断,第二种情况下与(1)相同利用全等三角形的性质可得,第三种情况相同.
解答 (1)证明:
∵BD⊥DE,CE⊥DE,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中
$\left\{\begin{array}{l}{∠BDA=∠CEA}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE;
(2)解:成立,证明如下:
∵∠BDA=∠AEC=∠BAC=a,
∴∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,
∴∠DBA=∠CAE,
在△ABD和△CAE中
$\left\{\begin{array}{l}{∠BDA=∠CEA}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE(AAS),
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE;
(3)当m⊥BC时,根据D和E重合,则DE=0,BD=CE;
当m与AC的夹角小于45°时,如图,
∵∠BAD+∠CAE=90°,直角△ABD中,∠ABD+∠BAD=90°,
∴∠CAE=∠ABD,
∴△ABD和△CAE中,$\left\{\begin{array}{l}{∠BDA=∠AEC=90°}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△CAE,
∴BD=AE,EC=AD,
又∵DE=AE-AD,
∴DE=BD-CE;
同理,当m与AC的夹角大于45°,小于90°时,DE=CE-BD.
点评 本题考查了全等三角形的判定与性质,正确分情况进行讨论,证明三角形全等是关键.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案| A. | -1 | B. | -2 | C. | ±1 | D. | ±2 |
| A. | 男、女生做代表的可能性一样大 | |
| B. | 男生做代表的可能性大 | |
| C. | 女生做代表的可能性大 | |
| D. | 男、女生做代表的可能性大小不能确定 |
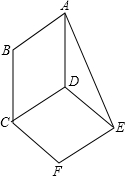 如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )
如图,?ABCD与?DCFE的周长相等,且∠BAD=60°,∠F=100°,则∠DAE的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
| A. | y=5x-3 | B. | y=-x-3 | C. | $y=\frac{3x-2}{2}$ | D. | y=5x+3 |