题目内容
20.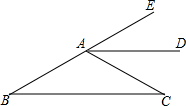 如图,已知∠B=∠C,AD∥BC.
如图,已知∠B=∠C,AD∥BC.(1)证明:AD平分∠CAE;
(2)如果∠BAC=120°,求∠B的度数.(不允许使用三角形内角和为180°)
分析 (1)根据AD∥BC,∠EAD=∠B,∠DAC=∠C,结合题干条件得到∠EAD=∠DAC,于是判定AD平分∠CAE;
(2)首先求出∠EAC的度数,然后根据角平分线的定义求出∠EAD的度数,再根据平行线的性质得到∠B的度数.
解答 (1)证明:∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C,
∵∠B=∠C,
∴∠EAD=∠DAC,
∴AD平分∠CAE;
(2)解:∵∠BAC=120°,
∴∠EAC=60°,
∵AD平分∠CAE,
∴∠EAD=$\frac{1}{2}$∠EAC=30°,
∵AD∥BC,
∴∠EAD=∠B,
∴∠B=30°.
点评 本题主要考查了平行线的性质以及角平分线的定义,解答本题的关键是熟练掌握两直线平行,同位角相等,两直线平行,内错角相等.

练习册系列答案
相关题目
11. 如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
 如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
15.下列说法错误的是( )
| A. | 5是25的算术平方根 | B. | ±4是64的立方根 | ||
| C. | (-4)3的立方根是-4 | D. | (-4)2的平方根是±4 |
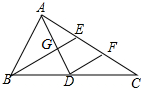 如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.
如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.