题目内容
4. 如图,矩形ABCD的边AB=4,BC=8,点P从A出发,以每秒2个单位沿A-B-C-D运动,同时点Q也从A出发,以每秒1个单位沿A-D运动,△APQ的面积为y,运动的时间为x秒,则y关于x的函数图象为( )
如图,矩形ABCD的边AB=4,BC=8,点P从A出发,以每秒2个单位沿A-B-C-D运动,同时点Q也从A出发,以每秒1个单位沿A-D运动,△APQ的面积为y,运动的时间为x秒,则y关于x的函数图象为( )| A. |  | B. | 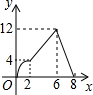 | C. | 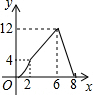 | D. |  |
分析 分情况探讨:当0≤x≤2时,P点在AB上,Q点在AD上;当2<x≤6时,P点在CB上,Q点在AD上;当6<x≤8时,P点在CD上,Q点在AD上;利用三角形面积进行计算得出函数解析式;进一步利用函数解析式选择答案即可.
解答 解:当0≤x≤2时,y=$\frac{1}{2}$•x•2x=x2;
当2<x≤6时,y=$\frac{1}{2}$×x×2=x;
当6<x≤8时,S=$\frac{1}{2}$×x×(16-2x)=-x2+8x.
符合题意的图象是A.
故选:A.
点评 此题主要考查了动点函数问题,三角形的面积计算,关键是根据x的取值范围表示出S与x之间的函数关系式.

练习册系列答案
相关题目
14.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A. | 3:4:3:4 | B. | 5:2:2:5 | C. | 2:3:4:5 | D. | 3:3:4:4 |
15.下列说法错误的是( )
| A. | 5是25的算术平方根 | B. | ±4是64的立方根 | ||
| C. | (-4)3的立方根是-4 | D. | (-4)2的平方根是±4 |
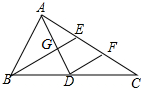 如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.
如图,在△ABC中,中线AD,BE相交于点G,过点D作DF∥BE交AC于点F,则$\frac{EF}{AC}$的值为$\frac{1}{4}$.