题目内容
10.计算:x+$\frac{1}{x-1}$+$\frac{{x}^{2}-3x+4}{1-{x}^{2}}$.分析 先通分,然后进行同分母分式加减运算,最后要注意将结果化为最简分式.
解答 解:原式=$\frac{x(1-{x}^{2})}{1-{x}^{2}}$-$\frac{1+x}{(1-x)(1+x)}$+$\frac{{x}^{2}-3x+4}{1-{x}^{2}}$
=$\frac{-{x}^{3}+{x}^{2}-3x+3}{(1-x)(1+x)}$
=$\frac{(1-x)({x}^{2}-3)}{(1-x)(1+x)}$
=$\frac{{x}^{2}-3}{1+x}$.
点评 本题考查了分式的加减,分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
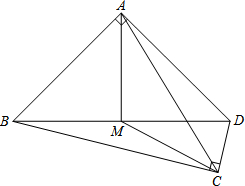 已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2.
已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2.