题目内容
13.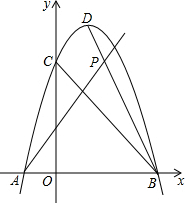 如图,已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,又tan∠OBC=1,过点A任作直线l交线段BD于点P,若点B、D到直线l的距离分别记为d1、d2,则d1+d2的最大值为$\sqrt{5}$.
如图,已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B(点B在X轴的正半轴上),与y轴交于点C,其顶点为D,又tan∠OBC=1,过点A任作直线l交线段BD于点P,若点B、D到直线l的距离分别记为d1、d2,则d1+d2的最大值为$\sqrt{5}$.
分析 易得AB的长度和点D到x轴的距离,由面积法得到AB•yD=AP•d1+AP•d2,由此可得d1+d2=$\frac{AB•{y}_{D}}{AP}$,过A作AM⊥BD于M,利用△ACD的面积可求得AM的长,在Rt△APM中,AP≥AM,故d1+d2≤$\frac{AB•{y}_{D}}{AM}$,而AB、yD、AM的长都已求得,由此可确定d1+d2的最大值.
解答 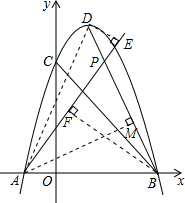 解:如图,过点A作AM⊥BD于M,过点B作BF⊥AP于F.过点D作DE⊥AP于E,则BF=d1,DE=d2.
解:如图,过点A作AM⊥BD于M,过点B作BF⊥AP于F.过点D作DE⊥AP于E,则BF=d1,DE=d2.
∵二次函数y=ax2+2x+3的图象与y轴交于点C,
∴令x=0,得y=3,
∴点C的坐标为(0,3),
∵tan∠OBC=$\frac{OC}{OB}$=1,
∴OB=OC=3,
∴点B的坐标为(3,0).
将其代入二次函数y=ax2+2x+3中,
可得:9a+6+3=0,
解得:a=-1,
∴二次函数的解析式为:y=-x2+2x+3=-(x-1)2+4,
∴二次函数y=ax2+2x+3的顶点D的坐标为(1,4),
∴AB=2(3-1)=4,BD=$\sqrt{(3-1)^{2}+(0-4)^{2}}$=2$\sqrt{5}$.
∴$\frac{1}{2}$AB•yD=$\frac{1}{2}$BD•AM=$\frac{1}{2}$AP•d1+AP•d2,即$\frac{1}{2}$×4×4=$\frac{1}{2}$×2$\sqrt{5}$×AM=$\frac{1}{2}$AP(d1+d2).
∴AM=$\frac{8\sqrt{5}}{5}$,d1+d2=$\frac{16}{AP}$.
∵AP≥AM,
∴d1+d2=$\frac{16}{AP}$≤$\frac{16}{AM}$,即d1+d2≤$\frac{16}{\frac{8\sqrt{5}}{5}}$=2$\sqrt{5}$,
∴d1+d2的最大值为2$\sqrt{5}$.
故答案是:2$\sqrt{5}$.
点评 此题主要考查了等腰直角三角形的性质、二次函数解析式的确定、函数图象交点坐标的求法、三角形面积的计算方法以及不等式的应用等重要知识,涉及知识面广,难度较大.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案| A. | 35 | B. | 36 | C. | 37 | D. | 38 |
| A. | 1.96×105 | B. | 1.96×104 | C. | 19.6×104 | D. | 0.196×106 |
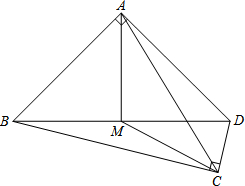 已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2.
已知,如图,四边形ABCD中,∠BAD=∠BCD=90°,M为BD的中点,AB=AD,BD=$2\sqrt{17}$,CD=2.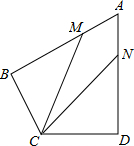 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则∠BCD=120°,cos∠MCN=$\frac{13}{14}$.
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则∠BCD=120°,cos∠MCN=$\frac{13}{14}$. 如图,已知△ABC和△DEF是全等的等边三角形,且它们的重合部分是等边三角形ABC的一半,求证:△AGI是等边三角形.
如图,已知△ABC和△DEF是全等的等边三角形,且它们的重合部分是等边三角形ABC的一半,求证:△AGI是等边三角形.