题目内容
14.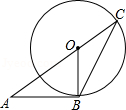 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C等于( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C等于( )| A. | 27° | B. | 36° | C. | 54° | D. | 60° |
分析 连接OB,根据切线的性质得到OB⊥AB,求出∠OBA=90°,根据三角形的内角和定理求出∠AOB的度数,由∠C和∠AOB是同弧所对的圆周角和圆心角,根据圆周角定理即可求出∠C.
解答 解:连接OB,
∵AB切圆O于B,
∴OB⊥AB,
∴∠OBA=90°,
∵∠A=36°,
∴∠AOB=180°-∠A-∠OBA=54°,
∵∠C和∠AOB是同弧所对的圆周角和圆心角,
∴∠C=$\frac{1}{2}$∠AOB=27°.
故选A.
点评 本题主要考查对三角形的内角和定理,垂线的定义,圆周角定理,切线的性质等知识点的理解和掌握,能灵活运用切线的性质和圆周角定理进行推理是解此题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
19.如图,搭第一个图形需要7根火柴棒.
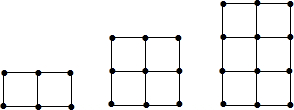
(1)搭一搭,填一填:
(2)搭n个图形需要5n+2根火柴棒.

(1)搭一搭,填一填:
| 第几个图形 | 1 | 2 | 3 | 4 | … |
| 火柴棒根数 | 7 | 12 | 17 | 22 | … |
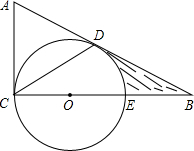 在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
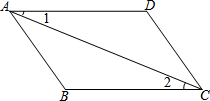 如图,已知∠1=∠2,∠B=∠D,试说明:AB∥CD
如图,已知∠1=∠2,∠B=∠D,试说明:AB∥CD