题目内容
5.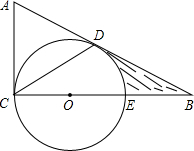 在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.(1)求证:△ACD为等边三角形;
(2)求图中阴影部分的面积(结果保留π和根号).
分析 (1)连接OD,求出∠ODB=90°,求出∠B=30°,∠DOB=60°,求出∠DCB度数,关键三角形内角和定理求出∠A,即可得出答案;
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案.
解答 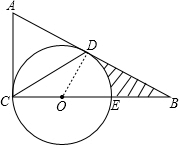 (1)证明:连接OD,
(1)证明:连接OD,
∵AB是⊙O切线,
∴∠ODB=90°,
∴BE=OE=OD=2,
∴∠B=30°,∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC=$\frac{1}{2}$∠DOB=30°,
∴∠ADC=90°-∠CDO=60°,
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∴∠A=∠ACD=∠ADC=60°,
∴△ACD为等边三角形;
(2)解:∵∠ODB=90°,OD=2,BO=2+2=4,
由勾股定理得:BD=2$\sqrt{3}$,
∴阴影部分的面积S=S△ODB-S扇形DOE=$\frac{1}{2}$×2$\sqrt{3}$×2-$\frac{60π{•2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2}{3}$π.
点评 本题考查了含30度角的直角三角形性质,勾股定理,扇形的面积,勾股定理,切线的性质等知识点的应用,主要考查学生综合性运用性质进行推理和计算的能力.

练习册系列答案
相关题目
17.已知点A(x1,y1),B(x2,y2)是反比例函数y=$\frac{5}{x}$图象上的点,若x1>0>x2,则一定成立的是( )
| A. | y1>0>y2 | B. | y1>y2>0 | C. | 0>y1>y2 | D. | y2>0>y1 |
18.在0,1,-1,π四个数中,最小的实数是( )
| A. | -1 | B. | π | C. | 0 | D. | 1 |
14.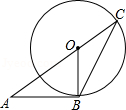 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C等于( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C等于( )
 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C等于( )
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=36°,则∠C等于( )| A. | 27° | B. | 36° | C. | 54° | D. | 60° |
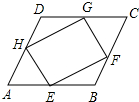 如图,在?ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:EFGH是平行四边形.
如图,在?ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:EFGH是平行四边形.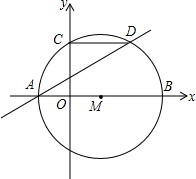 如图,⊙M的圆心M在x轴上,⊙M分别交x轴于点A、B(A在B的左边),交y轴的正半轴于点C,弦CD平行于x轴交⊙M于点D,已知A、B两点的横坐标分别是方程x2=4(x+3)的两个根.
如图,⊙M的圆心M在x轴上,⊙M分别交x轴于点A、B(A在B的左边),交y轴的正半轴于点C,弦CD平行于x轴交⊙M于点D,已知A、B两点的横坐标分别是方程x2=4(x+3)的两个根.