题目内容
8.某中学库存若干套桌椅,准备修理.现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修理桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元的修理费.(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a,由甲单独修理;b,由乙单独修理;c,甲、乙合作同时修理.你认为哪种方案省时又省钱?为什么?
分析 (1)通过理解题意可知本题的等量关系,即甲单独修完这些桌凳的天数=乙单独修完的天数+20天,列方程求解即可;
(2)分别求出三种方案的总费用,比较后即可得.
解答 解:(1)设该中学库存x套桌椅,
则甲需要$\frac{x}{16}$天,乙需要$\frac{x}{16+8}$天,
根据题意得:$\frac{x}{16}$-$\frac{x}{16+8}$=20,
解得:x=960,
答:该中学库存960套桌椅;
(2)方案a的费用为(80+10)×$\frac{960}{16}$=5400(元),
方案b的费用为(120+10)×$\frac{960}{16+8}$=5200(元),
方案c的费用为(80+120+10)×$\frac{960}{16+16+8}$=5040(元),
综上,方案c的费用省时又省力.
点评 本题考查了一元一次方程的应用,解题的关键是找到等量关系:甲单独修完这些桌凳的天数=乙单独修完的天数+20天.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
19.如图1,在边长为4的正△ABC中,点P以每秒1cm的速度从点A出发,沿折线AB-BC运动,到点C停止.过点P作PD⊥AC,垂足为D,PD的长度y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动5.5秒时,PD的长是( )
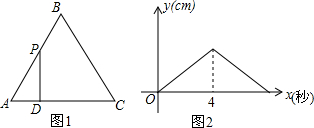

| A. | $\frac{5\sqrt{3}}{4}$cm | B. | $\frac{5\sqrt{3}}{2}$cm | C. | 2$\sqrt{3}$cm | D. | 3$\sqrt{3}$cm |
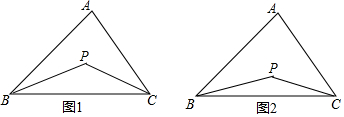 【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?
【提出问题】已知如图1,P是∠ABC、∠ACB的角平分线的交点,你能找到∠P、∠A的关系吗?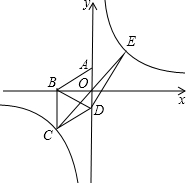 如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.
如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C. 如图所示,直线AD和BC被直线AB所截,∠1和∠2是同位角;∠4、∠FAC与∠2也是同位角.
如图所示,直线AD和BC被直线AB所截,∠1和∠2是同位角;∠4、∠FAC与∠2也是同位角.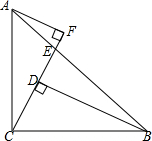 已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.
已知:如图,Rt△ABC中,AC=BC,∠ACB=90°,CF交AB于点E,BD⊥CF于点D,AF⊥CF.