题目内容
1.抛物线y=-x2+2(m-1)x-2n的顶点为A(1,3),求m,n的值.分析 根据抛物线y=-x2+2(m-1)x-2n的顶点为A(1,3),可知-$\frac{2(m-1)}{2×(-1)}$=1,$\frac{4×(-1)×(-2n)-[2(m-1)]^{2}}{4×(-1)}$=3,从而可以得到m、n的值.
解答 解:∵抛物线y=-x2+2(m-1)x-2n的顶点为A(1,3),
∴-$\frac{2(m-1)}{2×(-1)}$=1,$\frac{4×(-1)×(-2n)-[2(m-1)]^{2}}{4×(-1)}$=3,
解得m=2,n=-1.
点评 本题考查二次函数的性质,解题的关键是掌握二次函数的顶点坐标公式.

练习册系列答案
相关题目
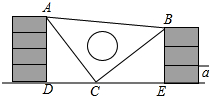 课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.
课间,小明拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示.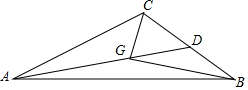 如图,点G是△ABC的重心,连结AG,BG,CG,并延长AG交BC于点D,若AG=13,BG=12,CG=5,则BD的长为6.5.
如图,点G是△ABC的重心,连结AG,BG,CG,并延长AG交BC于点D,若AG=13,BG=12,CG=5,则BD的长为6.5.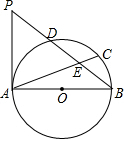 如图所示,AB为⊙O的直径,D为$\widehat{AC}$的中点,AC、BD交于点E,P为BD延长线上一点,且PD=DE.
如图所示,AB为⊙O的直径,D为$\widehat{AC}$的中点,AC、BD交于点E,P为BD延长线上一点,且PD=DE.