题目内容
16.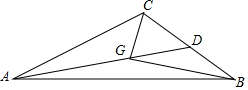 如图,点G是△ABC的重心,连结AG,BG,CG,并延长AG交BC于点D,若AG=13,BG=12,CG=5,则BD的长为6.5.
如图,点G是△ABC的重心,连结AG,BG,CG,并延长AG交BC于点D,若AG=13,BG=12,CG=5,则BD的长为6.5.
分析 延长AD至E,使DE=GD,连接CE、BE,根据重心的性质求出DG,根据平行四边形的判定定理得到四边形CGBE是平行四边形,得到GE=2GD=13,BE=CG=5,根据勾股定理的逆定理得到△GBE是直角三角形,根据直角三角形的性质解答即可.
解答 解: 延长AD至E,使DE=GD,连接CE、BE,
延长AD至E,使DE=GD,连接CE、BE,
∵点G是△ABC的重心,
∴GD=$\frac{1}{2}$AG=6.5,D是BC的中点,又DE=GD,
∴四边形CGBE是平行四边形,GE=2GD=13,
∴BE=CG=5,
∵GB2+BE2=144+25=169,GE2=169,
∴GB2+BE2=GE2,
∴△GBE是直角三角形,又DE=DG,
∴BD=$\frac{1}{2}$GE=6.5,
故答案为:6.5.
点评 本题考查的是三角形的重心的概念和性质,三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11. 有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
 有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )
有理数a、b、c在数轴上的位置如图所示,化简|a-b|+|c-a|-|b-c|的结果是( )| A. | -2a | B. | -2b | C. | -2a-2b | D. | 2a-2b |
 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,则在数轴上A、B两点之间的距离AB=|a-b|.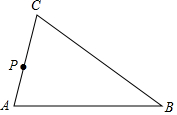 如图,在△ABC中,点P为AC上一点,请利用尺规在BC边上求作一点Q,使得△ABC∽△QPC(保留作图痕迹,不写作法)
如图,在△ABC中,点P为AC上一点,请利用尺规在BC边上求作一点Q,使得△ABC∽△QPC(保留作图痕迹,不写作法)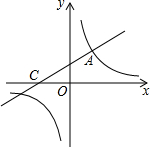 直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).
直线y=$\frac{1}{2}$x+2与双曲线y=$\frac{k}{x}$相交于点A(2,3).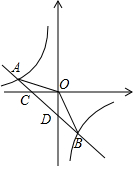 如图,在平面直角坐标系中,一次函数y=ax-1(a≠0)的图象与x轴交于点C,与y轴交于点D,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,点B的坐标是(3,m),连接OB,tan∠BOD=$\frac{3}{4}$.
如图,在平面直角坐标系中,一次函数y=ax-1(a≠0)的图象与x轴交于点C,与y轴交于点D,与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二、四象限内的A、B两点,点B的坐标是(3,m),连接OB,tan∠BOD=$\frac{3}{4}$.