题目内容
17.如果反比例函数y=$\frac{3-4a}{x}$的图象在每一个象限内y随x的增大而增大,那么a满足的条件是a>$\frac{3}{4}$.分析 根据反比例函数的性质可得3-4a<0,再解不等式即可.
解答 解:∵反比例函数y=$\frac{3-4a}{x}$每一个象限内y随x的增大而增大,
∴3-4a<0,
解得:a>$\frac{3}{4}$,
故答案为:a>$\frac{3}{4}$.
点评 本题考查了反比例函数的性质.对于反比例函数y=$\frac{k}{x}$,当k>0时,在每一个象限内,函数值y随自变量x的增大而减小;当k<0时,在每一个象限内,函数值y随自变量x增大而增大.

练习册系列答案
相关题目
12.计算(-3)×(-1)2的结果等于( )
| A. | 3 | B. | -2 | C. | -3 | D. | 1 |
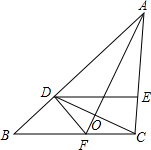 已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.
已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.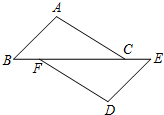 如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AB=DE.
如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AB=DE.