题目内容
19. 点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.
点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
分析 连接AC,利用三角形中位线定理可证明EF∥AC,EF=$\frac{1}{2}$AC,HG∥AC,HG=$\frac{1}{2}$AC,所以EF$\underset{∥}{=}$HG,即四边形EFGH是平行四边形.
解答  证明:连接AC,
证明:连接AC,
∵点E,F别是四边形ABCD的边AB,BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
同理:HG∥AC,HG=$\frac{1}{2}$AC,
∴EF$\underset{∥}{=}$HG,
∴四边形EFGH是平行四边形.
点评 此题主要考查了三角形中位线定理和平行四边形的判定方法,题目比较典型,又有综合性,难度不大,解题的关键是正确的添加辅助线,把四边形的问题转化为三角形的问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.9的平方根等于( )
| A. | -3 | B. | 3 | C. | ?±3 | D. | $\sqrt{3}$ |
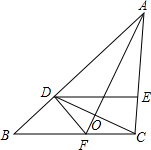 已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.
已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.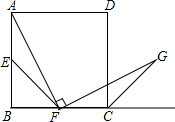 如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.
如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.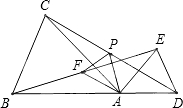 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点B、A、D在同一条直线上,连接BE、CD,F、P分别为BE、CD的中点,连接AF、AP、PF.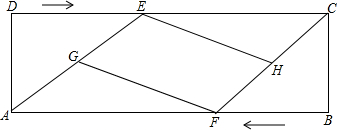
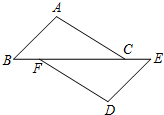 如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AB=DE.
如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AB=DE.