题目内容
10.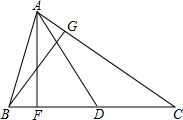 如图,△ABC的边BC上的高为AF,中线为AD,AC边上的高为BG,已知AF=6,BC=10,BG=5.
如图,△ABC的边BC上的高为AF,中线为AD,AC边上的高为BG,已知AF=6,BC=10,BG=5.(1)求△ABC的面积;
(2)求AC的长;
(3)说明△ABC和△ACD的面积关系.
分析 (1)直接利用三角形的面积计算方法计算得出答案即可;
(2)利用三角形的面积计算公式建立方程求得答案即可;
(3)利用三角形的面积计算公式以及两个三角形底和高的关系得出答案即可.
解答 解:(1)∵△ABC的边BC上的高为AF,AF=6,BC=10,
∴△ABC的面积=$\frac{1}{2}$BC•AF=$\frac{1}{2}$×10×6=30;
(2)∵AC边上的高为BG,BG=5,
∴△ABC的面积=$\frac{1}{2}$AC•BG=30,
∴AC=12;
(3)∵△ABC的中线为AD,
∴BC=2CD,
∴S△ABC=2S△ACD.
点评 此题考查三角形的面积计算公式,掌握三角形的面积=$\frac{1}{2}$×底×高是解决问题的关键.

练习册系列答案
相关题目
20.下列语句好可以称为命题的是( )
| A. | 延长线段AB到C | B. | 垂线段最短 | ||
| C. | 过点P作线段AB的垂线 | D. | 锐角都相等吗 |
19.直线y=-3x+1上有一点P,且点P到y轴的距离是1,则点P的坐标为( )
| A. | (1,-2) | B. | (-1,4) | C. | (1,-2)或(-1,4) | D. | 以上都不对 |
20.下列各式没有意义的是( )
| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{-5}$ | D. | $\sqrt{(-5)^{2}}$ |
 如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.
如图,已知AC与BD相交于点O,AD∥BC,且AO=OD.求证:OB=OC.