题目内容
6. 小青家有一块如图的四边形土地要流转出去,其中∠D=∠B=90°,∠C=135°,用激光测距仪测得:BC=$\sqrt{2}$(千米),DC=3$\sqrt{2}$(千米),求这块四边形土地的面积.
小青家有一块如图的四边形土地要流转出去,其中∠D=∠B=90°,∠C=135°,用激光测距仪测得:BC=$\sqrt{2}$(千米),DC=3$\sqrt{2}$(千米),求这块四边形土地的面积.
分析 延长AD、BC相交于E,证出△DCE和△ABE都是等腰直角三角形,四边形ABCD的面积=△ABE的面积-△DCE的面积,然后求出即可.
解答 解:延长AD、BC相交于E,如图: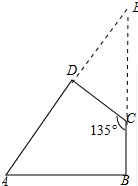
∵∠ADC=∠B=90°,∠BCD=135°,
∴∠A=360°-90°-90°-135°=45°,∠CDE=90°,
∴△DCE和△ABE都是等腰直角三角形,
∴DE=DC=3$\sqrt{2}$,AB=BE,
∴CE=$\sqrt{2}$DC=6,
∴AB=BE=BC+CE=$\sqrt{2}$+6,
∴四边形ABCD的面积=△ABE的面积-△DCE的面积=$\frac{1}{2}$×($\sqrt{2}$+6)2-$\frac{1}{2}$×(3$\sqrt{2}$)2=10+6$\sqrt{2}$(平方千米).
点评 本题考查了勾股定理的应用、等腰直角三角形的判定与性质;熟练掌握勾股定理,证出三角形是等腰直角三角形是解决问题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
1.一元二次方程(x-1)(x+2)=0的两根是( )
| A. | -1,2 | B. | 1,2 | C. | 1,-2 | D. | -1,-2 |
11.在某学校组织的环保知识竞赛中,每班参加比赛的人数相同,成绩分别为A,B,C,D四个等级,其中相应等级的得分一次记为:100分,90分,80分,70分,学校将某年级一班和二班的成绩整理并绘制成如下的统计图:

请你根据图表提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为21;
(2)请你将表格补充完整:
(3)如果学校要选出某班参加比赛的一半学生,代表学校参加全市比赛,应该从哪个班级挑选合适?请说明理由.

请你根据图表提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为21;
(2)请你将表格补充完整:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | 87.6 | 90 | 90 |
| 二班 | 87.6 | 80 | 100 |

 小智和小慧想知道学校旗杆AB的高度,他们发现旗杆上的绳子从顶端垂到地面还多了1米(图1),即BC=1米,当他们往外把绳子拉直,发现绳子下端刚好接触地面时,触点D离旗杆下端B的距离为5米(图2),于是,小智和小慧很快算出了旗杆的高度,你能推算出旗杆的高度吗?请写出过程.
小智和小慧想知道学校旗杆AB的高度,他们发现旗杆上的绳子从顶端垂到地面还多了1米(图1),即BC=1米,当他们往外把绳子拉直,发现绳子下端刚好接触地面时,触点D离旗杆下端B的距离为5米(图2),于是,小智和小慧很快算出了旗杆的高度,你能推算出旗杆的高度吗?请写出过程. 某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地.当人和木板对湿地的压力一定时,人和木板对地面的压强P(Pa)随着木板面积S(m2)的变化而变化情况如图,试根据所提供的信息,回答下列问题:
某校科技小组进行野外考察,利用铺垫木板的方式通过了一片烂泥湿地.当人和木板对湿地的压力一定时,人和木板对地面的压强P(Pa)随着木板面积S(m2)的变化而变化情况如图,试根据所提供的信息,回答下列问题: 如图,小明家有一块长1.50m,宽1m的矩形地毯,为了使地毯美观,小明请来工匠在地毯的四周镶上宽度相同的花色地毯,镶完后地毯的面积是原地毯面积的2倍.则花色地毯的宽为0.25m.
如图,小明家有一块长1.50m,宽1m的矩形地毯,为了使地毯美观,小明请来工匠在地毯的四周镶上宽度相同的花色地毯,镶完后地毯的面积是原地毯面积的2倍.则花色地毯的宽为0.25m.