题目内容
9.已知⊙O中弦AB⊥弦CD,垂足为H.(1)如图1,当AB为直径时,求证:BC=BD;
(2)如图2,当tan∠ACD=$\frac{1}{2}$,且BO=$\frac{5}{2}$$\sqrt{5}$时,求BC的长;
(3)如图3,在(2)的条件下,若AB=CB,过H作BD的垂线垂足为E,直线HE交AC于点F,交⊙O于点G,求△OFH的面积.
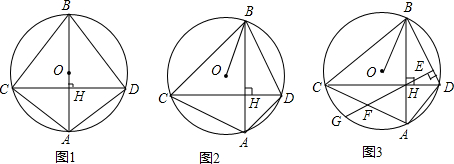
分析 (1)由AB为直径,CD为弦,且直径与弦垂直,利用垂径定理得到B为$\widehat{CD}$中点,得到两条弧相等,利用等弧对等弦即可得证;
(2)连接OC,过O作OR垂直于BC,设∠ACD=x,利用同弧所对的圆周角定理得到一对角相等,表示出∠ABD=x,进而表示出∠BDC,进而表示出∠BOC,由OB=OC,利用等边对等角得到一对角相等,根据tan∠ACD与BO的值,求出BR的值,利用垂径定理即可确定出BC的值;
(3)连接OF、OH,过O作OM⊥AB于点M,ON⊥AC于点N,设AH=x,则有CH=2x,表示出BH,利用勾股定理求出x的值,求出AM与OM长,得出OH的长,进而利用勾股定理求出ON与FH的长,即可求出三角形OFH的面积.
解答 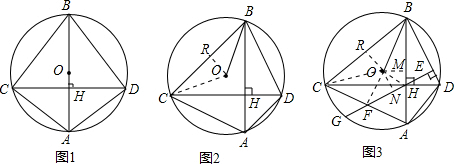 (1)证明:∵AB为直径,且AB⊥弦CD,
(1)证明:∵AB为直径,且AB⊥弦CD,
∴$\widehat{BC}$=$\widehat{BD}$,
∴BC=BD;
(2)解:如图2,连接OC,过O作OR⊥BC于点R,
设∠ACD=x,
∵$\widehat{AD}$=$\widehat{AD}$,
∴∠ACD=∠ABD=x,
∵AB⊥CD,
∴∠BDC=90°-x,
∵$\widehat{BC}$=$\widehat{BC}$,
∴∠BOC=2∠BDC=180°-2x,
∵OB=OC,
∴∠OBC=∠OCB=x,
∴tan∠OBC=tan∠ACD=$\frac{1}{2}$,
∵BO=$\frac{5\sqrt{5}}{2}$,
∴BR=2OR=5,
∵OR⊥BC,
∴BC=2BR=10;
(3)解:如图3,连接OF、OH,过O作OM⊥AB于点M,ON⊥EF于点N,
设AH=x,则CH=2x,
∵BA=BC=10,
∴BH=10-x,
在Rt△BCH中,由勾股定理解得:x=4,
∴AM=5,OM=2.5,
∴OH=$\frac{\sqrt{29}}{2}$,
∵OE⊥BD,
∴∠EHD=∠DBH=∠ACD=∠CHF,
∴HF为△ACH的斜边中线,
∴HF=$\frac{1}{2}$AC,
∴AC=4$\sqrt{5}$,
∴CF=HF=2$\sqrt{5}$,
在Rt△COF中得OF=$\frac{3\sqrt{5}}{2}$,
令HN=a,则FN=2$\sqrt{5}$-a,
由勾股定理:ON2=OF2-FN2=OH2-NH2,
解得:a=$\frac{4\sqrt{5}}{5}$,
∴ON=$\frac{9\sqrt{5}}{10}$,
∴△OFH的面积为$\frac{9\sqrt{5}}{10}$×2$\sqrt{5}$×$\frac{1}{2}$=$\frac{9}{2}$.
点评 此题属于圆的综合题,涉及的知识有:圆周角定理,勾股定理,直角三角形斜边上的中线性质,垂径定理,以及锐角三角函数定义,熟练掌握定理及性质是解本题的关键.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 一个靶子如图所示,已知中心10环的半径r=10cm,9环的半径R1=20cm,8环的半径R2=40cm,如果每发子弹都打在靶上并取得环数.
一个靶子如图所示,已知中心10环的半径r=10cm,9环的半径R1=20cm,8环的半径R2=40cm,如果每发子弹都打在靶上并取得环数. 甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题: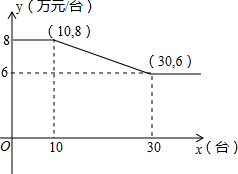 某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.
某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.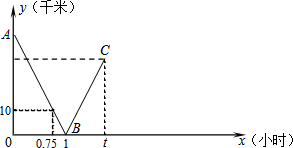 小明、小王二人骑车在平直的公路上分别从甲、乙两地相向而行,两人同时出发,匀速行驶.设行驶的时间为x(时),两人之间的距离为y(千米),小明到达乙地后立刻返回甲地,小王到达甲地后停止行驶,图中的折线表示从两人出发至小明到达乙地过程中y与x之间的函数关系.
小明、小王二人骑车在平直的公路上分别从甲、乙两地相向而行,两人同时出发,匀速行驶.设行驶的时间为x(时),两人之间的距离为y(千米),小明到达乙地后立刻返回甲地,小王到达甲地后停止行驶,图中的折线表示从两人出发至小明到达乙地过程中y与x之间的函数关系.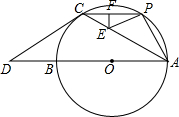 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.
如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,已知CD=CA.