题目内容
5．
如图，直线AB∥CD，EF⊥CE，垂足为E，EF交CD于点F，∠1=48°，则∠2的度数是（ ）| A． | 42° | B． | 48° | C． | 52° | D． | 58° |
分析 由垂线的性质和直角三角形的性质求出∠C的度数，再由平行线的性质即可得出结果．
解答 解：∵EF⊥CE，
∴∠CEF=90°，
∴∠C=90°-∠1=90°-48°=42°，
∵AB∥CD，
∴∠2=∠C=42°；
故选：A．
点评 本题考查了平行线的性质、直角三角形的性质；熟练掌握平行线的性质，由直角三角形的性质求出∠C是解决问题的关键．
练习册系列答案
相关题目
如图所示，A、B之间是一座山，一条铁路要通过A、B两地，在A地测得铁路走向是北偏东48°25′，则在B地测得A地在南偏西多少度？如果A、B两地同时开工，那么在B地按∠β施工，∠β为多少度才能使铁路在山腹中准确接通？
如图，一个圆柱体和一个长方体组成的几何体，则其主视图是（ ）
如图，AB∥DC，AD∥BC，E为BC延长线上一点，连结AE与CD相交于点F，若∠CFE=∠E． 试说明AE平分∠BAD．
20．
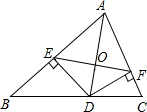如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，则下列结论：
①OA=OD；
②AD⊥EF；
③AE+DF=AF+DE；
④当∠BAC=90°时，四边形AEDF是正方形．
其中一定正确的是（ ）
如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高，则下列结论：①OA=OD；
②AD⊥EF；
③AE+DF=AF+DE；
④当∠BAC=90°时，四边形AEDF是正方形．
其中一定正确的是（ ）
| A． | ①②③ | B． | ②③④ | C． | ①③④ | D． | ①②③④ |
如图，已知AB∥CD，AC平分∠DAB，且∠DCA=28°，∠B=96°．
14．下列各式中不能用平方差公式计算的是（ ）
| A． | （a+b）（-a+b） | B． | （a2+1）（a2-1） | C． | （-2x+1）（-2x-1） | D． | （x-y）（y-x） |