题目内容
5.抛物线y=ax2+bx-8与x轴交于A、B,与y轴交于C,D为抛物线的顶点,AB=2,D点的横坐标为3.(1)求抛物线的解析式;
(2)若H为射线DA与y轴的交点,N为射线AB上一点,设N点的横坐标为t,△DHN的面积为S,求S与t的函数关系式;
(3)在(2)的条件下,G为线段DH上一点,过G作y轴的平行线交抛物线于F,Q为抛物线上一点,连接GN、NQ、AF、GF,若NG=NQ,NG⊥NQ,且∠AGN=∠FAG,求GF的长.

分析 (1)先求出A、B两点坐标,再利用待定系数法即可解决问题.
(2)如图1中,连接OD,根据S=S△OND+S△ONH-S△OHD计算即可.
(3)如图2中,延长FG交OB于M,只要证明△MAF≌△MGB,得FM=BM.设M(m,0),列出方程即可解决问题.
解答 解:(1)∵抛物线y=ax2+bx-8与x轴交于A、B,与y轴交于C,D为抛物线的顶点,AB=2,D点的横坐标为3,
∴A(2,0),B(4,0),
∴$\left\{\begin{array}{l}{4a+2b-8=0}\\{16a+4b-8=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=6}\end{array}\right.$,
∴抛物线解析式为y=-x2+6x-8;
(2)如图1中,连接OD.抛物线顶点D坐标(3,1),H(0,-2).
∵S=S△OND+S△ONH-S△OHD=$\frac{1}{2}$×t×1+$\frac{1}{2}$×t×2-$\frac{1}{2}$×2×3=$\frac{3}{2}$t-3.
∴S=$\frac{3}{2}$x-3;
(3)如图2中,延长FG交OB于M.
∵OH=OA,
∴∠OAH=∠OHA=45°,
∵FM∥OH,
∴∠MGA=∠OHA=∠MAG=45°,
∴MG=MA,
∵∠FAG=∠NGA,
∴∠MAF=∠MGN,
在△MAF和△MGN中,
$\left\{\begin{array}{l}{∠AMF=∠GMB}\\{AM=MG}\\{∠MAF=∠MGB}\end{array}\right.$,
∴△MAF≌△MGB,
∴FM=BM.设M(m,0),
∴-(-m2+6m-8)=4-m,
解得m=1或4(舍弃),
∴FM=3,MG=1,
∴GF=FM-MG=2.
点评 本题考查二次函数综合题、全等三角形的判定和性质、待定系数法等知识,解题的关键是学会利用分割法求面积.学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案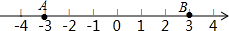 如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )
如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | -3.14 | B. | 0 | C. | 1 | D. | 2 |
| A. | k<3 | B. | k≤3 | C. | k>3 | D. | k≥3 |
 如图,在直角坐标系中,△ABC与△DEF全等,其中A、B、C的对应点分别为D、E、F,且AB=BC.若A点的坐标为(-3,4),B(-6,0),C(-1,0),D、E两点在y轴上,E点坐标为(0,-1),则F点的坐标为(4,2).
如图,在直角坐标系中,△ABC与△DEF全等,其中A、B、C的对应点分别为D、E、F,且AB=BC.若A点的坐标为(-3,4),B(-6,0),C(-1,0),D、E两点在y轴上,E点坐标为(0,-1),则F点的坐标为(4,2). 如图,A,B是数轴上的两点,在线段AB上任取一点C,则点C到原点的距离不大于2的概率是$\frac{2}{3}$.
如图,A,B是数轴上的两点,在线段AB上任取一点C,则点C到原点的距离不大于2的概率是$\frac{2}{3}$.