题目内容
4. 如图,在圆心角为90°的扇形OAB中,半径OA=4cm,C为弧AB的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为( )cm2.
如图,在圆心角为90°的扇形OAB中,半径OA=4cm,C为弧AB的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为( )cm2.| A. | 4π-2$\sqrt{2}$-2 | B. | 4π-2 | C. | 2π+2$\sqrt{2}$-2 | D. | 2π+2$\sqrt{2}$ |
分析 连接OC、EC,由△OCD≌△OCE、OC⊥DE可得DE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,分别求出S扇形OBC、S△OCD、S△ODE面积,根据S扇形OBC+S△OCD-S△ODE=S阴影部分可得.
解答 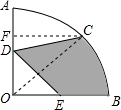 解:连结OC,过C点作CF⊥OA于F,
解:连结OC,过C点作CF⊥OA于F,
∵半径OA=4,C为$\widehat{AB}$的中点,D、E分别是OA、OB的中点,
∴OD=OE=2,OC=4,∠AOC=45°,
∴CF=2$\sqrt{2}$,
∴空白图形ACD的面积=扇形OAC的面积-三角形OCD的面积
=$\frac{45π×{4}^{2}}{360}$-$\frac{1}{2}$×2×2$\sqrt{2}$
=2π-2$\sqrt{2}$,
三角形ODE的面积=$\frac{1}{2}$OD×OE=2,
∴图中阴影部分的面积=扇形OAB的面积-空白图形ACD的面积-三角形ODE的面积
=$\frac{90π×{4}^{2}}{360}$-(2π-2$\sqrt{2}$)-2
=2π+2$\sqrt{2}$-2.
故选C.
点评 考查了扇形面积的计算,本题难点是得到空白图形ACD的面积,关键是理解图中阴影部分的面积=扇形OAB的面积-空白图形ACD的面积-三角形ODE的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.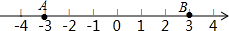 如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )
如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )
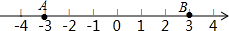 如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )
如图,数轴上两点A、B在线段AB上任意取一点C,则点C到表示1的距离不大于2的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
9.下列四个数中,最小的数是( )
| A. | -2 | B. | -1 | C. | 0 | D. | $\sqrt{2}$ |
13.四个数-3.14,0,1,2,最大的数是( )
| A. | -3.14 | B. | 0 | C. | 1 | D. | 2 |
 如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,那么折痕AB的长为2$\sqrt{3}$cm.
如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,那么折痕AB的长为2$\sqrt{3}$cm. 如图,在直角坐标系中,△ABC与△DEF全等,其中A、B、C的对应点分别为D、E、F,且AB=BC.若A点的坐标为(-3,4),B(-6,0),C(-1,0),D、E两点在y轴上,E点坐标为(0,-1),则F点的坐标为(4,2).
如图,在直角坐标系中,△ABC与△DEF全等,其中A、B、C的对应点分别为D、E、F,且AB=BC.若A点的坐标为(-3,4),B(-6,0),C(-1,0),D、E两点在y轴上,E点坐标为(0,-1),则F点的坐标为(4,2).