题目内容
11.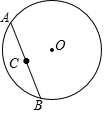 如图,AB为⊙O的弦,点C为AB的中点,AB=6,当点A、B在⊙O上运动一周时,点C所走过的路径与⊙O围成的图形面积是9π.
如图,AB为⊙O的弦,点C为AB的中点,AB=6,当点A、B在⊙O上运动一周时,点C所走过的路径与⊙O围成的图形面积是9π.
分析 根据题意知点C所走过的路径为小圆O,由垂径定理得OC⊥AB,且BC=$\frac{1}{2}$AB=3,从而得出点C所走过的路径与⊙O围成的图形面积是πOB2-π•OC2=π(OB2-OC2)=π•BC2=9π.
解答 解:如图,连接OC、OB,
点C所走过的路径为小圆O,
∵点C为AB的中点,AB=6,
∴OC⊥AB,且BC=$\frac{1}{2}$AB=3,
∴点C所走过的路径与⊙O围成的图形面积是πOB2-π•OC2=π(OB2-OC2)=π•BC2=9π,
故答案为:9π.
点评 本题主要考查垂径定理和扇形的面积计算,熟练掌握垂径定理是解题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE.
如图,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE.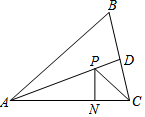 如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=$\sqrt{6}$,若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是$\frac{3\sqrt{2}}{2}$.
如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=$\sqrt{6}$,若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是$\frac{3\sqrt{2}}{2}$.