题目内容
19. 如图,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE.
如图,在?ABCD中,点E在BC边上,AE=AB,点F在DE上,∠DAF=∠CDE.(1)△AEF∽△DEA,并证明:
(2)如果AB=6,DF=5,求EF的长.
分析 (1)由AB=AE得到∠B=∠1,再利用平行四边形的性质得AD∥BC,∠B=∠ADC,所以∠1=∠DAE,则∠DAE=∠ADC,于是可得到∠2=∠3,然后根据相似三角形的判定方法可判定△AEF∽△DEA;
(2)利用△AEF∽△DEA得到AE:EF=ED:AE,则可得到关于EF的一元二次方程,然后解方程即可.
解答 解:(1)△AEF∽△DEA.理由如下:
∵AB=AE,
∴∠B=∠1,
∵四边形ABCD为平行四边形,
∴AD∥BC,∠B=∠ADC,
∴∠1=∠DAE,
∴∠DAE=∠ADC,
即∠2+∠DAF=∠3+∠CDE,
∵∠DAF=∠CDE,
∴∠2=∠3,
而∠AEF=∠DEA,
∴△AEF∽△DEA;
故答案为△DEA;
(2)∵AB=6,
∴AE=6,
∵△AEF∽△DEA,
∴AE:EF=ED:AE,即6:EF=(EF+5):6,
整理得EF2+5EF-36=0,解得EF=-9(舍去)或EF=4,
即EF的长为4.
点评 本题考查了三角形相似的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在运用相似三角形的性质时,主要利用相似进行几何计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.股民小杨上星期五买进某公司股票1000股,每股20元,如表为本周内每日该股票的涨跌情况(单位:元):
(1)星期三收盘时,该股票涨或跌了多少元?
(2)本周内该股票的最高价是每股多少元?最低价是每股多少元?
(3)已知小杨买进股票时付了1.5‰的手续费,卖出时还需要付成交额的2‰作为手续费和交易税.如果小杨在星期五收盘前将全部股票卖出,则他的收益情况如何?
(说明:2‰表示千分之二)
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +2.20 | +1.42 | -0.80 | -2.52 | +1.30 |
(2)本周内该股票的最高价是每股多少元?最低价是每股多少元?
(3)已知小杨买进股票时付了1.5‰的手续费,卖出时还需要付成交额的2‰作为手续费和交易税.如果小杨在星期五收盘前将全部股票卖出,则他的收益情况如何?
(说明:2‰表示千分之二)

 试试你的作图能力.画出△ABC关于x轴对称的图形△A′B′C′,写出△A′B′C′各顶点坐标.
试试你的作图能力.画出△ABC关于x轴对称的图形△A′B′C′,写出△A′B′C′各顶点坐标.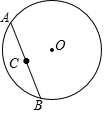 如图,AB为⊙O的弦,点C为AB的中点,AB=6,当点A、B在⊙O上运动一周时,点C所走过的路径与⊙O围成的图形面积是9π.
如图,AB为⊙O的弦,点C为AB的中点,AB=6,当点A、B在⊙O上运动一周时,点C所走过的路径与⊙O围成的图形面积是9π.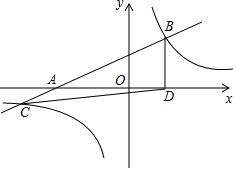 如图,一次函数y=kx+2的图象与x轴交于点A,与反比例函数$y=\frac{m}{x}$的图象交于点B(2,3)和点C.
如图,一次函数y=kx+2的图象与x轴交于点A,与反比例函数$y=\frac{m}{x}$的图象交于点B(2,3)和点C.