题目内容
6.观察下列等式:第1个等式:a1=$\frac{1}{1×3}$=$\frac{1}{2}$×(1-$\frac{1}{3}$);
第2个等式:a2=$\frac{1}{3×5}$=$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$);
第3个等式:a3=$\frac{1}{5×7}$=$\frac{1}{2}$×($\frac{1}{5}$-$\frac{1}{7}$);
第4个等式:a4=$\frac{1}{7×9}$=$\frac{1}{2}$×($\frac{1}{7}$-$\frac{1}{9}$)…
请解答下列问题:
(1)用含有n(n为正整数)的式子表示第n个等式;
(2)求a1+a2+a3+a4+…+a100的值.
分析 (1)由已知等式知,连续奇数乘积的倒数等于各自倒数差的一半,据此可得;
(2)根据以上规律可得原式=$\frac{1}{2}$×(1-$\frac{1}{3}$)+$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$×($\frac{1}{7}$-$\frac{1}{9}$)+…+$\frac{1}{2}$($\frac{1}{199}$-$\frac{1}{201}$)=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{199}$-$\frac{1}{201}$),即可得出答案.
解答 解:(1)由已知等式知,连续奇数乘积的倒数等于各自倒数差的一半,
∴第n个等式为$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$);
(2)原式=$\frac{1}{2}$×(1-$\frac{1}{3}$)+$\frac{1}{2}$×($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$×($\frac{1}{7}$-$\frac{1}{9}$)+…+$\frac{1}{2}$($\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{199}$-$\frac{1}{201}$)
=$\frac{1}{2}$×(1-$\frac{1}{201}$)
=$\frac{1}{2}$×$\frac{200}{201}$
=$\frac{100}{201}$.
点评 本题主要考查数字的变化规律,根据题意得出连续奇数乘积的倒数等于各自倒数差的一半且掌握裂项求和是解题的关键.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | -3 | B. | 0 | C. | 1 | D. | 2 |
 如图,△ABC中,点D为AB的中点,E在边AC上,将△ADE沿过DE折叠,使点A落在BC上F处,若∠B=40°,则∠BDF=100度.
如图,△ABC中,点D为AB的中点,E在边AC上,将△ADE沿过DE折叠,使点A落在BC上F处,若∠B=40°,则∠BDF=100度.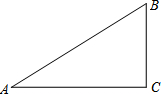 已知:如图,在△ABC中,∠A=30°,∠B=60°.
已知:如图,在△ABC中,∠A=30°,∠B=60°.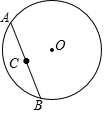 如图,AB为⊙O的弦,点C为AB的中点,AB=6,当点A、B在⊙O上运动一周时,点C所走过的路径与⊙O围成的图形面积是9π.
如图,AB为⊙O的弦,点C为AB的中点,AB=6,当点A、B在⊙O上运动一周时,点C所走过的路径与⊙O围成的图形面积是9π. 将下列各数表示在数轴上,并用“<”连接.
将下列各数表示在数轴上,并用“<”连接.