题目内容
解不等式:
>0.
| (x-3)(x+2) |
| (x+3)(x-2) |
考点:一元一次不等式组的应用
专题:
分析:根据有理数除法法则分两种情况:①
或②
,然后通过解不等式组即可求解.
|
|
解答:解:由题意,可得:①
或②
,
解不等式组①得,x>3或x<-3.
解不等式组②得-2<x<2,
故原不等式的解集为x>3或x<-3或-2<x<2.
|
|
解不等式组①得,x>3或x<-3.
解不等式组②得-2<x<2,
故原不等式的解集为x>3或x<-3或-2<x<2.
点评:本题考查了一元一次不等式组的应用,解题关键是根据有理数除法法则分情况进行讨论.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=24cm,BC=12cm.点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤12).
如图,在矩形ABCD中,AB=24cm,BC=12cm.点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤12).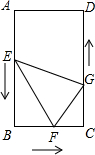 如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=DC=12cm,BC=AD=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向运动.点F、G的速度为2m/s,点E的速度为4m/s,设移动开始后第ts时,△EFG的面积为S(cm2).
如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=DC=12cm,BC=AD=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向运动.点F、G的速度为2m/s,点E的速度为4m/s,设移动开始后第ts时,△EFG的面积为S(cm2).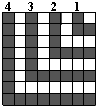 如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成.图中,第1个黑色形由3个正方形组成,第2个黑色形由7个正方形组成,那么组成第12个黑色形的正方形个数是( )
如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成.图中,第1个黑色形由3个正方形组成,第2个黑色形由7个正方形组成,那么组成第12个黑色形的正方形个数是( )