题目内容
11.如图,在平面直角坐标系中,AB是⊙M的直径弦CD⊥AB于点O,点E是BC上的一点,且AC=CE.(1)求证:∠ACG=∠CAG;
(2)当∠ACG=30°,MA=4时,求点C和点E坐标;
(3)在(2)的条件下,点P在$\widehat{EBD}$上运动时,是否存在一点P使得四边形GDPE的面积最大?如果存在,求出点P的坐标和最大面积的值;不存在,请说明理由.

分析 (1)利用垂径定理和圆的有关性质即可得出结论;
(2)利用圆周角和圆心角的关系,得出△ACM是等边三角形,即可求出点C坐标,再求出∠EMI,即可求出点E坐标,
(3)先判断出DE过点M,再判断出四边形DGEP面积最大时PG垂直DE且过点M,再用三角形的面积公式即可.
解答 解:(1)∵AB是⊙M的直径弦CD⊥AB于点O,
∴OC⊥AB,
∴$\widehat{AC}$=$\widehat{AD}$,
∵AC=CE.
∴$\widehat{AC}$=$\widehat{CE}$,
∴$\widehat{AC}=\widehat{AD}=\widehat{CE}$,
∴∠ACG=∠CAG,
(2)如图1,连接MC,ME,过点E作EI⊥AB,
在Rt△AOC中,∵∠ACO=30°,
∴∠CAM=60°,
∵MA=MC,
∴△ACM是等边三角形,
∵MA=4,
∴OM=$\frac{1}{2}$AM=2,OC=$\frac{\sqrt{3}}{2}$AM=2$\sqrt{3}$,
∴C(0,2$\sqrt{3}$)
∵AC=CE,
∴∠CME=∠AMC=60°,
∴∠EMI=60°,
∴∠MEI=30°,
∴MI=$\frac{1}{2}$ME=2,EI=2$\sqrt{3}$.
∴OI=OM+MI=4,
∴E(4,2$\sqrt{3}$);
(3)如图2,连接DE,AD,PG.过点P作PN⊥AB,
由(1)知,$\widehat{AC}=\widehat{AD}=\widehat{CE}$,
∴∠CDG=∠AED=∠ACG=∠AEC=30°,
∴DG=EG,∠DAE=90°,
∴DE过点M,
∵使得四边形GDPE的面积最大,
∴PG过点M且PG⊥DE,
∵∠CDE=30°,
∴∠OMD=60°,
∴∠PMN=∠OMG=30°,
在Rt△PMN中,∠PMN=30°PM=4,
∴PN=2,MN=2$\sqrt{3}$,
∴P(2$\sqrt{3}$,-2),在Rt△OMG中,∠OMG=30°,
∴MG=$\sqrt{3}$,
∴S四边形GDPE=S△DGE+S△PDE=$\frac{1}{2}$×DE×MG+$\frac{1}{2}$×DE×PM=$\frac{1}{2}$×8×$\sqrt{3}$+$\frac{1}{2}$×8×4=4$\sqrt{3}$+16.
即:四边形GDPE的面积最大时,点P的坐标(2$\sqrt{3}$,-2),最大面积的值4$\sqrt{3}$+16.
点评 此题是圆的综合题,主要考查了圆的性质,垂径定理,等边三角形的判定和性质,含30°的直角三角形的性质,解本题的关键是判断出△ACM是等边三角形.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C-A-B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).
如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C-A-B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).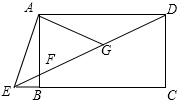 如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为2$\sqrt{3}$.
如图,四边形ABCD是矩形,点E在线段CB的延长线上,连接DE交AB于点F,∠AED=2∠CED,点G是DF的中点,若BE=2,DF=8,则AB的长为2$\sqrt{3}$.