题目内容
3.已知A(2,m),B(n,-1)是双曲线y=-$\frac{6}{x}$上的两点,求△AOB的面积.分析 将点A与B的坐标分别代入双曲线的解析式求出A、B两点的坐标,然后作图求△AOB的面积即可.
解答 解:∵A(2,m),B(n,-1)是双曲线y=-$\frac{6}{x}$上的两点,
∴2m=-6,-n=-6
∴m=-3,n=6
∴A(2,-3),B(6,-1)
如下图所示:作BN⊥x轴于点N,作AM⊥y轴于点M,BC⊥y轴于点C,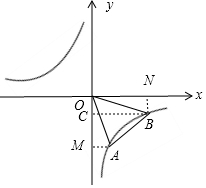
则:S△AOB=S矩形ONBC+S梯形ABCM-S△OAM-S△OBN=6×1+$\frac{1}{2}$(2+6)×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×6×1=8
即:△AOB的面积为5
点评 本题考查了反比例函数系数k的几何意义,解题的关键是求出出A、B两点的坐标,将S△AOB看作是S矩形ONBC+S梯形ABCM-S△OAM-S△OBN.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
8.下列方程中,你最喜欢的一个一元二次方程是( )
| A. | $\frac{1}{4}{x^2}$-x=9 | B. | x3-x2+40=0 | C. | $\frac{4}{x-1}$=3 | D. | 3x3-2xy+y2=0 |

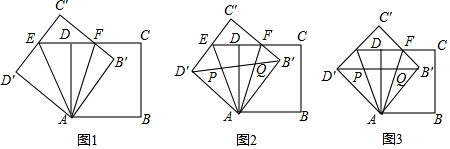

 如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系? AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°.
AB、CD相交于点O,DE是△DOB的角平分线,若∠B=∠C,∠A=52°,则∠EDB=26°.