题目内容
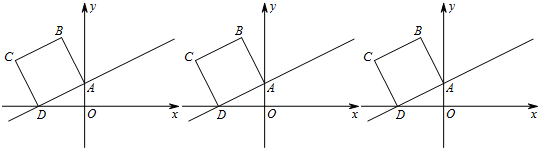
19.如图,在平面直角坐标系中,已知点A(0,1)、D(-2,0),作直线AD并以线段AD为一边向上作正方形ABCD.(1)填空:点B的坐标为(-1,3),点C的坐标为(-3,2).
(2)若正方形以每秒$\sqrt{5}$个单位长度的速度沿射线DA向上平移,直至正方形的顶点C落在y轴上时停止运动.在运动过程中,设正方形落在y轴右侧部分的面积为S,求S关于平移时间t(秒)的函数关系式,并写出相应的自变量t的取值范围.
分析 (1)过点B作BB′⊥y轴于点B′,过点C作CC′⊥x轴于点C′,由全等三角形的性质可知AB′=CC′=DO,BB′=DC′=AO,结合各边的关系即可找出B、C点的坐标;
(2)按图形的变化分成三部分:①用时间t表示出直角三角形两直角边长度,套用三角形面积公式即可得出结论;②用时间t表示出直角梯形上、下底与高的长度,套用梯形的面积公式即可得出结论;③由正方形的面积减去剩下直角三角形的面积即可得出结论.
解答 解:(1)过点B作BB′⊥y轴于点B′,过点C作CC′⊥x轴于点C′,如图1所示.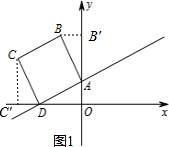
∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠CDA=90°.
∵BB′⊥y轴,
∴∠BB′A=90°,
∴∠BAB′+∠DAO=180°-∠BAD=90°,∠BAB′+∠ABB′=90°,
∴∠DAO=∠ABB′.
在△ABB′和△DAO中,
$\left\{\begin{array}{l}{∠DAO=∠ABB′}\\{∠AB′B=∠DOA=90°}\\{AB=AD}\end{array}\right.$,
∴△ABB′≌△DAO(AAS);
同理△CDC′≌△DAO.
∴AB′=CC′=DO,BB′=DC′=AO.
∵点A(0,1)、D(-2,0),
∴AB′=CC′=DO=2,BB′=DC′=AO=1,
∴OB′=OA+AB′=3,OC′=OD+DC′=3,BB′=1,CC′=2,
故点B的坐标为(-1,3),点C的坐标为(-3,2).
故答案为:(-1,3);(-3,2).
(2)AB=BC=CD=DA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
整个运动过程分成三部分:
①点B没有运动到y轴右侧时,如图1所示.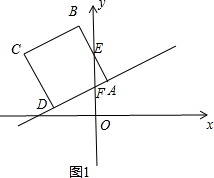
其中AF=$\sqrt{5}$t,AE=2$\sqrt{5}$t,
此时0<AE≤AB,即0<2$\sqrt{5}$t≤$\sqrt{5}$,
解得:0<t≤$\frac{1}{2}$.
S=$\frac{1}{2}$AF•AE=5t2;
②点B运动到了y轴右侧,点D还未运动到y轴右侧,过B作BM∥y轴,交AD于点M,如图2所示.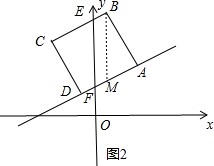
其中AF=$\sqrt{5}$t,AM=$\frac{1}{2}$AB=$\frac{\sqrt{5}}{2}$,BE=MF=AF-AM=$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$,
此时AM<AF≤AD,即$\frac{\sqrt{5}}{2}$<$\sqrt{5}$t≤$\sqrt{5}$,
解得:$\frac{1}{2}$<t≤1.
S=$\frac{1}{2}$(BE+AF)AB=$\frac{1}{2}×(\sqrt{5}t+\sqrt{5}t-\frac{\sqrt{5}}{2})×\sqrt{5}$=5t-$\frac{5}{4}$;
③点D运动到了y轴右侧,点C还未运动到y轴右侧,过C作CM∥y轴交直线AD于点M,令CD与y轴的交点为N,如图3所示.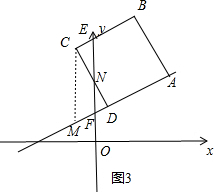
其中AF=$\sqrt{5}$t,DM=$\frac{1}{2}$CD=$\frac{\sqrt{5}}{2}$,CE=MF=AD+DM-AF=$\frac{3\sqrt{5}}{2}$-$\sqrt{5}$t,DF=AF-AD=$\sqrt{5}$t-$\sqrt{5}$,
∵∠NCE=∠NDF=90°,∠CNE=∠DNF,
∴△CNE∽△DNF,
∴$\frac{CN}{DN}=\frac{CE}{DF}$,
又∵CN+DN=$\sqrt{5}$,
∴CN=$\frac{3-2t}{2t-2}$DN,CN=3$\sqrt{5}$-2$\sqrt{5}$t.
此时AD<AF≤AM,即$\sqrt{5}$<$\sqrt{5}$t≤$\frac{3\sqrt{5}}{2}$,
解得:1<t≤$\frac{3}{2}$.
S=AB•AD-$\frac{1}{2}$CE•CN=$\sqrt{5}×\sqrt{5}-\frac{1}{2}×(\frac{3\sqrt{5}}{2}-\sqrt{5}t)×(3\sqrt{5}-2\sqrt{5}t)$=-5t2+15t-$\frac{25}{4}$.
综上可知:S关于平移时间t(秒)的函数关系式为S=$\left\{\begin{array}{l}{5{t}^{2}(0<t≤\frac{1}{2})}\\{5t-\frac{5}{4}(\frac{1}{2}<t≤1)}\\{-5{t}^{2}+15t-\frac{25}{4}(1<t≤\frac{3}{2})}\end{array}\right.$.
点评 本题考查了正方形的性质、全等三角形的判定及性质、一元一次不等式的应用、三角形的面积公式以及直角梯形的面积公式,解题的关键:(1)由全等三角形的性质找出△ABB′和CC′D各边的长度;(2)解一元一次不等式找出不同情况下t的取值范围.本题属于中档题,(1)难度不大,由于是填空题,可以不用去证三角形全等省去不少时间;(2)难度不大,但是过程繁琐,做题过程中不仅用到了解一元一次不等式找x的取值范围,还用到了三角形、直角梯形的面积公式,故在解决该题型题目时,细心观察图形,通过图形的变化分类是关键.

(1)解分式方程一定会产生增根;(2)方程$\frac{x-2}{{{x^2}-4x+4}}$=0的根为x=2;(3)x+$\frac{1}{x-1}$=1+$\frac{1}{x-1}$是分式方程.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | 10$\sqrt{5}$ | B. | 11$\sqrt{5}$ | C. | 12$\sqrt{5}$ | D. | 13$\sqrt{5}$ |
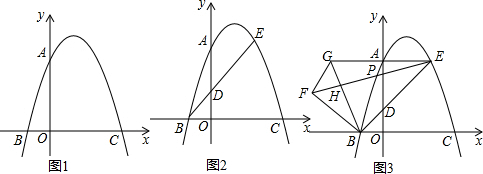
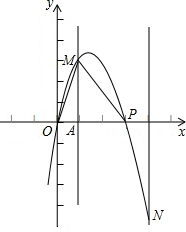 如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位长度的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.
如图,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位长度的速度运动t秒(t>0),抛物线y=-x2+bx+c经过点O和点P.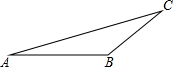 如图,在△ABC中,∠B=135°,tanA=$\frac{2}{5}$,BC=6$\sqrt{2}$.
如图,在△ABC中,∠B=135°,tanA=$\frac{2}{5}$,BC=6$\sqrt{2}$. 如图,在△ABC中,CD⊥AB,垂直为点D,F为BC上一点,FG⊥AB,垂足为点G,E为AC上一点,连结DE,且∠1=∠2,求证:DE∥BC.
如图,在△ABC中,CD⊥AB,垂直为点D,F为BC上一点,FG⊥AB,垂足为点G,E为AC上一点,连结DE,且∠1=∠2,求证:DE∥BC.