题目内容
如图,Rt△ACB≌Rt△ACO,点A在第二象限内,点B,C在x轴的负半轴上,OA=4,∠CAO=30°.
(1)求点C的坐标;
(2)如图1,将△ACB绕点C按顺时针方向旋转30°到△A′CB′的位置,其中A′C交直线OA于点E,A′B′分别交直线OA,CA于点F,G,请求出线段A′E的长度;
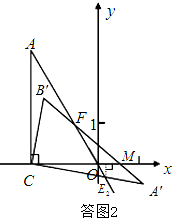
(3)在图2的基础上,将△A′CB′绕点C按顺时针方向继续旋转,当△COE的面积为
时,求直线CE的函数表达式.

(1)求点C的坐标;
(2)如图1,将△ACB绕点C按顺时针方向旋转30°到△A′CB′的位置,其中A′C交直线OA于点E,A′B′分别交直线OA,CA于点F,G,请求出线段A′E的长度;
(3)在图2的基础上,将△A′CB′绕点C按顺时针方向继续旋转,当△COE的面积为
| ||
| 4 |

考点:待定系数法求一次函数解析式,勾股定理,旋转的性质,解直角三角形
专题:
分析:(1)首先在Rt△ACO中,根据∠CAO=30°解直角三角形可以得到OA,OC的长,然后就可以得到点C的坐标;
(2)根据已知条件容易得到△CEO为等边三角形,即可知CE长度,然后根据勾股定理可得AC的长度,再利用旋转的性质可知AC=A′C,即可求得A′E;
(3)过点E1作E1M⊥OC于点M,利用S△COE1=4和∠E1OM=60°可以求出点E1的坐标,然后利用待定系数法确定直线CE的解析式.此题有两种情况,分别是E在第二或四象限里.
(2)根据已知条件容易得到△CEO为等边三角形,即可知CE长度,然后根据勾股定理可得AC的长度,再利用旋转的性质可知AC=A′C,即可求得A′E;
(3)过点E1作E1M⊥OC于点M,利用S△COE1=4和∠E1OM=60°可以求出点E1的坐标,然后利用待定系数法确定直线CE的解析式.此题有两种情况,分别是E在第二或四象限里.
解答:解:(1)∵在Rt△ACO中,∠CAO=30°,OA=4,
∴OC=2,
∴C点的坐标为(-2,0).
(2)根据题意可知∠ACA′=30°,
∴∠A′CO=60°,
∵∠AOC=90°-∠CAO=30°,
∴△CEO为等边三角形,
∴CE=CO=2,
根据旋转的性质可得:AC=A′C,
∵AC2+CO2=AO2,
∴AC=2
,
∴A′E=A′C-CE=2
-2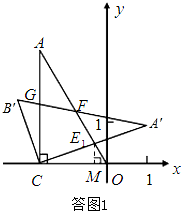
(3)如答图1,过点E1作E1M⊥OC于点M.
∵S△COE1=
CO•E1M=
,
∴E1M=
.
∵在Rt△E1MO中,∠E1OM=60°,则
,
∴tan60°=
,
∴OM=
,
∴点E1的坐标为(-
,
).
设直线CE1的函数表达式为y=k1x+b1,则
,
 解得
解得
.
∴y=
x+
.
同理,如答图2所示,点E2的坐标为(
,-
).
设直线CE2的函数表达式为y=k2x+b2,则
,
解得
.
∴y=-
x-
.
∴OC=2,
∴C点的坐标为(-2,0).
(2)根据题意可知∠ACA′=30°,
∴∠A′CO=60°,
∵∠AOC=90°-∠CAO=30°,
∴△CEO为等边三角形,
∴CE=CO=2,
根据旋转的性质可得:AC=A′C,
∵AC2+CO2=AO2,
∴AC=2
| 3 |
∴A′E=A′C-CE=2
| 3 |

(3)如答图1,过点E1作E1M⊥OC于点M.
∵S△COE1=
| 1 |
| 2 |
| ||
| 4 |
∴E1M=
| ||
| 4 |
∵在Rt△E1MO中,∠E1OM=60°,则
|
∴tan60°=
| E1M |
| OM |
∴OM=
| 1 |
| 4 |
∴点E1的坐标为(-
| 1 |
| 4 |
| ||
| 4 |
设直线CE1的函数表达式为y=k1x+b1,则
|
 解得
解得
|
∴y=
| ||
| 7 |
2
| ||
| 7 |
同理,如答图2所示,点E2的坐标为(
| 1 |
| 4 |
| ||
| 4 |
设直线CE2的函数表达式为y=k2x+b2,则
|
解得
|
∴y=-
| ||
| 9 |
2
| ||
| 9 |
点评:考查了直角三角形、一次函数.此题是开放性试题,把直角三角形、一次函数等知识综合在一起,要求学生对这些知识比较熟练,利用几何方法解决代数问题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
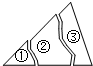 如图,有一块三角形的玻璃,不小心掉在地上打成三块,现要到玻璃店重新划一块与原来形状、大小一样的玻璃,只需带第( )块到玻璃店去.
如图,有一块三角形的玻璃,不小心掉在地上打成三块,现要到玻璃店重新划一块与原来形状、大小一样的玻璃,只需带第( )块到玻璃店去. 如图,在?ABCD中,AC、BD相交于O,EF过O分别交AD、BC于E、F,GH过O分别交AB、CD于G、H,试证明四边形EGFH是平行四边形.
如图,在?ABCD中,AC、BD相交于O,EF过O分别交AD、BC于E、F,GH过O分别交AB、CD于G、H,试证明四边形EGFH是平行四边形. 如图,双曲线y=
如图,双曲线y=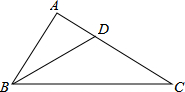 已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.
已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.