题目内容
 如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=
如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=| 4 |
| 3 |
(1)求AC的长和点D的坐标;
(2)求证:
| FE |
| EC |
| AE |
| DC |
(3)当△EFC为等腰三角形时,求△AEC的面积.
考点:相似形综合题
专题:
分析:(1)利用矩形的性质,在Rt△ABC中,利用三角函数求出AC、BC的长度,从而得到A点坐标;由点D与点A关于y轴对称,进而得到D点的坐标;
(2)欲证
=
;只需证明△AEF与△DCE相似,只需要证明两个对应角相等即可.如图①,在△AEF与△DCE中,易知∠CDE=∠CAO,∠AEF=∠DCE,从而问题解决;
(3)当△EFC为等腰三角形时,有三种情况,需要分类讨论:
①当CE=EF时,此时△AEF与△DCE相似比为1,则有AE=CD;求出E点坐标,计算出面积.
②当EF=FC时,此时△AEF与△DCE相似比为
,则有AE=
CD;求出E点坐标,计算出面积.
③当CE=CF时,F点与A点重合,这与已知条件矛盾,故此种情况不存在.
(2)欲证
| FE |
| EC |
| AE |
| DC |
(3)当△EFC为等腰三角形时,有三种情况,需要分类讨论:
①当CE=EF时,此时△AEF与△DCE相似比为1,则有AE=CD;求出E点坐标,计算出面积.
②当EF=FC时,此时△AEF与△DCE相似比为
| 6 |
| 5 |
| 5 |
| 6 |
③当CE=CF时,F点与A点重合,这与已知条件矛盾,故此种情况不存在.
解答: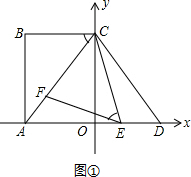 解:(1)由题意tan∠ACB=
解:(1)由题意tan∠ACB=
,
∴cos∠ACB=
,
∵四边形ABCO为矩形,AB=16,
∴BC=12,AB=20,
∴A点坐标为(-12,0),
∵点D与点A关于y轴对称,
∴D(12,0).
(2)点D与点A关于y轴对称,∴∠CDE=∠CAO,
∵∠CEF=∠ACB,∠ACB=∠CAO,
∴∠CDE=∠CEF,
又∵∠AEC=∠AEF+∠CEF=∠CDE+∠DCE(三角形外角性质)
∴∠AEF=∠DCE.
则在△AEF与△DCE中,∠CDE=∠CAO,∠AEF=∠DCE,
∴△AEF∽△DCE.
∴
=
;
(3)当△EFC为等腰三角形时,有以下三种情况:
①当CE=EF时,
∵△AEF∽△DCE,
∴△AEF≌△DCE
∴AE=CD=20,
 ∴OE=AE-OA=20-12=8,
∴OE=AE-OA=20-12=8,
∴E(8,0);
∴△AEC的面积为
AE•OC=
×20×16=160.
②当EF=FC时,如图②所示,过点F作FM⊥CE于M,则点M为CE中点,
∴CE=2ME=2EF•cos∠CEF=2EF•cos∠ACB=
EF.
∵△AEF∽△DCE,
∴
=
,即:
=
,
解得:AE=
,
∴OE=AE-OA=
,
∴E(
,0).
∴△AEC的面积为
AE•OC=
×16×
=
.
③当CE=CF时,则有∠CFE=∠CEF,
∵∠CEF=∠ACB=∠CAO,
∴∠CFE=∠CAO,即此时E点与D点重合,这与已知条件矛盾.
∴△AEC的面积为160或者
.
 解:(1)由题意tan∠ACB=
解:(1)由题意tan∠ACB=| 4 |
| 3 |
∴cos∠ACB=
| 3 |
| 5 |
∵四边形ABCO为矩形,AB=16,
∴BC=12,AB=20,
∴A点坐标为(-12,0),
∵点D与点A关于y轴对称,
∴D(12,0).
(2)点D与点A关于y轴对称,∴∠CDE=∠CAO,
∵∠CEF=∠ACB,∠ACB=∠CAO,
∴∠CDE=∠CEF,
又∵∠AEC=∠AEF+∠CEF=∠CDE+∠DCE(三角形外角性质)
∴∠AEF=∠DCE.
则在△AEF与△DCE中,∠CDE=∠CAO,∠AEF=∠DCE,
∴△AEF∽△DCE.
∴
| FE |
| EC |
| AE |
| DC |
(3)当△EFC为等腰三角形时,有以下三种情况:
①当CE=EF时,
∵△AEF∽△DCE,
∴△AEF≌△DCE
∴AE=CD=20,
 ∴OE=AE-OA=20-12=8,
∴OE=AE-OA=20-12=8,∴E(8,0);
∴△AEC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
②当EF=FC时,如图②所示,过点F作FM⊥CE于M,则点M为CE中点,
∴CE=2ME=2EF•cos∠CEF=2EF•cos∠ACB=
| 6 |
| 5 |
∵△AEF∽△DCE,
∴
| EF |
| CE |
| AE |
| ED |
| EF | ||
|
| AE |
| 20 |
解得:AE=
| 50 |
| 3 |
∴OE=AE-OA=
| 14 |
| 3 |
∴E(
| 14 |
| 3 |
∴△AEC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 50 |
| 3 |
| 400 |
| 3 |
③当CE=CF时,则有∠CFE=∠CEF,
∵∠CEF=∠ACB=∠CAO,
∴∠CFE=∠CAO,即此时E点与D点重合,这与已知条件矛盾.
∴△AEC的面积为160或者
| 400 |
| 3 |
点评:本题综合考查了矩形、等腰三角形、直角三角形等平面几何图形在坐标平面内的性质与变换,相似三角形的判定与性质应用是其核心.难点在于第(3)问,当△EFC为等腰三角形时,有三种情况,需要分类讨论,注意不要漏解,继而求得面积.

练习册系列答案
相关题目
 将一个半径为9,圆心角为120°的扇形,卷成一个如图形状的圆锥(无重叠),则这个圆锥底面圆的半径是( )
将一个半径为9,圆心角为120°的扇形,卷成一个如图形状的圆锥(无重叠),则这个圆锥底面圆的半径是( )| A、1 | B、2 | C、3 | D、π |
 如图:⊙M在直角坐标系中,圆心M在y轴正半轴上,弧AB所对的圆心角是120°,⊙M的半径是2cm.
如图:⊙M在直角坐标系中,圆心M在y轴正半轴上,弧AB所对的圆心角是120°,⊙M的半径是2cm. 如图,在△ABC中,∠ACB=90°,D在AC上,且AD=BC,E在CB的延长线上且BE=AC,连接DE交AB于F,则∠BFE的度数为
如图,在△ABC中,∠ACB=90°,D在AC上,且AD=BC,E在CB的延长线上且BE=AC,连接DE交AB于F,则∠BFE的度数为