题目内容
 如图,在△ABC中,∠ACB=90°,D在AC上,且AD=BC,E在CB的延长线上且BE=AC,连接DE交AB于F,则∠BFE的度数为
如图,在△ABC中,∠ACB=90°,D在AC上,且AD=BC,E在CB的延长线上且BE=AC,连接DE交AB于F,则∠BFE的度数为考点:全等三角形的判定与性质,等腰直角三角形,平行四边形的判定与性质
专题:计算题
分析:过E作EG⊥CE,使EG=AD,根据AD=BC,等量代换得到BC=EG,再由AC=BE,且夹角为直角,利用SAS得到三角形ABC与三角形BGE全等,利用全等三角形的对应边相等得到AB=GB,∠CAB=∠EBG,利用同角的余角相等得到∠EBG与∠ABC互余,进而得到∠ABG为直角,进而得到三角形ABG为等腰直角三角形,得到∠BAG=45°,根据AD与GE平行且相等得到四边形ADEG为平行四边形,进而得到AG与DE平行,利用两直线平行同位角相等求出∠BFE的度数.
解答: 解:过E作EG⊥CE,使EG=AD,
解:过E作EG⊥CE,使EG=AD,
∵AD=BC,
∴BC=GE,
在△ABC和△BGE中,
,
∴△ABC≌△BGE(SAS),
∴AB=GB,∠CAB=∠EBG,
∵∠CAB+∠ABC=90°,
∴∠EBG+∠ABC=90°,
∴∠ABG=90°,
∴△ABG为为等腰直角三角形,
∴∠BAG=45°,
∵AD∥GE,AD=GE,
∴四边形ADEG为平行四边形,
∴DE∥AG,
∴∠BFE=∠BAG=45°.
故答案为:45°
 解:过E作EG⊥CE,使EG=AD,
解:过E作EG⊥CE,使EG=AD,∵AD=BC,
∴BC=GE,
在△ABC和△BGE中,
|
∴△ABC≌△BGE(SAS),
∴AB=GB,∠CAB=∠EBG,
∵∠CAB+∠ABC=90°,
∴∠EBG+∠ABC=90°,
∴∠ABG=90°,
∴△ABG为为等腰直角三角形,
∴∠BAG=45°,
∵AD∥GE,AD=GE,
∴四边形ADEG为平行四边形,
∴DE∥AG,
∴∠BFE=∠BAG=45°.
故答案为:45°
点评:此题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,以及平行四边形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=
如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB= 双曲线y1、y2在第一象限的象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
双曲线y1、y2在第一象限的象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为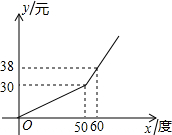 电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电
电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电