题目内容
1.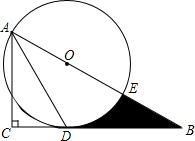 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
分析 (1)连接OD,根据平行线判定推出OD∥AC,推出OD⊥BC,根据切线的判定推出即可;
(2)①根据含有30°角的直角三角形的性质得出OB=2OD=2r,AB=2AC=3r,从而求得半径r的值;②根据S阴影=S△BOD-S扇形DOE求得即可.
解答  解:(1)直线BC与⊙O相切;
解:(1)直线BC与⊙O相切;
连结OD,∵OA=OD,
∴∠OAD=∠ODA,
∵∠BAC的角平分线AD交BC边于D,
∴∠CAD=∠OAD,
∴∠CAD=∠ODA,
∴OD∥AC,
∴∠ODB=∠C=90°,
即OD⊥BC.
又∵直线BC过半径OD的外端,
∴直线BC与⊙O相切.
(2)设OA=OD=r,在Rt△BDO中,∠B=30°,
∴OB=2r,
在Rt△ACB中,∠B=30°,
∴AB=2AC=6,
∴3r=6,解得r=2.
(3)在Rt△ACB中,∠B=30°,
∴∠BOD=60°.
∴$S_{扇形ODE}^{\;}=\frac{{60π•{2^2}}}{360}=\frac{2}{3}π$.
∵∠B=30°,OD⊥BC,
∴OB=2OD,
∴AB=3OD,
∵AB=2AC=6,
∴OD=2,BD=2$\sqrt{3}$
S△BOD=$\frac{1}{2}$×OD•BD=2$\sqrt{3}$,
∴所求图形面积为$S_{△BOD}^{\;}-S_{扇形ODE}^{\;}=2\sqrt{3}-\frac{2}{3}π$.
点评 本题考查了切线的判定,含有30°角的直角三角形的性质,扇形的面积等知识点的应用,主要考查学生的推理能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.方程:$\frac{2}{x}$+$\frac{3}{{x}^{2}}$=1的解是( )
| A. | x=-1 | B. | x=3 | C. | x=-1或x=3 | D. | x=1或x=-312 |
9.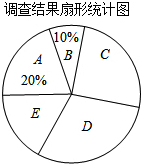 2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表.
2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表.
请根据图表中提供的信息解答下列问题:
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)安庆市人口现有6200万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
 2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表.
2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表. | 组别 | 焦点话题 | 频数(人数) |
| A | 食品安全 | 80 |
| B | 教育医疗 | m |
| C | 就业养老 | n |
| D | 生态环保 | 120 |
| E | 其他 | 60 |
(1)填空:m=40,n=100.扇形统计图中E组所占的百分比为15%;
(2)安庆市人口现有6200万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
13.下列事件中,为必然事件的是( )
| A. | 购买一张彩票,中奖 | |
| B. | 一个袋中只装有2个黑球,从中摸出一个球是黑球 | |
| C. | 抛掷一枚硬币,正面向上 | |
| D. | 打开电视,正在播放广告 |
11.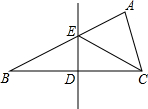 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
 如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )
如图,在△ABC中,BA=BC,∠B=30°,BC的垂直平分线交AB于E,垂足为D,若ED=1,则EC的长为( )| A. | 1 | B. | 1+$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
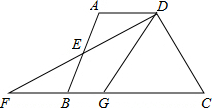 如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.