题目内容
18.关于x的一元二次方程(a-1)x2+2ax-3+a=0有实数根,则a的取值范围是a≥$\frac{3}{4}$,且a≠1.分析 由一元二次方程(a-1)x2+2ax-3+a=0有实数根,则a-1≠0,即a≠1,且△≥0,即△=(2a)2-4(a-1)(-3+a)=16a-12≥0,然后解两个不等式得到a的取值范围.
解答 解:∵关于x的一元二次方程(a-1)x2+2ax-3+a=0有实数根,
∴△=(2a)2-4(a-1)(-3+a)=16a-12≥0,且a-1≠0,
∴a≥$\frac{3}{4}$,且a≠1.
故答案为:a≥$\frac{3}{4}$,且a≠1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了一元二次方程的定义.

练习册系列答案
相关题目
 已知如图,∠BAC=∠BPC,AP平分∠CAN,PN⊥AB于点N,PM⊥AC于M,求$\frac{AC+AB}{CM}$的值.
已知如图,∠BAC=∠BPC,AP平分∠CAN,PN⊥AB于点N,PM⊥AC于M,求$\frac{AC+AB}{CM}$的值.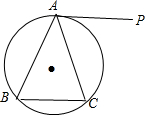 如图,⊙0是△ABC的外接圆,AB=AC,AP∥BC,直线AP是否与⊙O相切?为什么?
如图,⊙0是△ABC的外接圆,AB=AC,AP∥BC,直线AP是否与⊙O相切?为什么?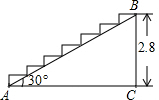 如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元.
如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元.