题目内容
3.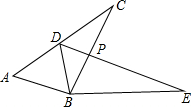 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.(1)若∠ABE=162°,∠DBC=30°,求∠CBE的度数;
(2)求△DCP与△BPE的周长和.
分析 (1)根据全等三角形的性质得到∠ABC=∠DBE,计算即可;
(2)根据全等三角形的性质求出BE、DE,根据三角形的周长公式计算即可.
解答 解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AD+DC=4.8,BE=BC=4.1,
△DCP和△BPE的周长和=DC+DP+BP+BP+PE+BE=DC+DE+BC+BE=15.4.
点评 本题考查的是全等三角形的性质、三角形内角和定理的应用,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
8.下列各组数中,是互为相反数的一组是( )
| A. | -3和$\sqrt{(-3)^{2}}$ | B. | $\sqrt{(-3)}$和-$\frac{1}{3}$ | C. | -3和$\root{3}{-27}$ | D. | $\root{3}{27}$和|-3| |
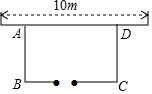 如图,用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为10m,其中一边BC留一道1m宽的门.
如图,用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为10m,其中一边BC留一道1m宽的门. 如图,△ABC中,点D,E分别在边AB,AC上,∠ADE=∠C,∠BAC的平分线AG分别交线段DE,BC于点F,G.
如图,△ABC中,点D,E分别在边AB,AC上,∠ADE=∠C,∠BAC的平分线AG分别交线段DE,BC于点F,G.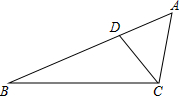 已知△ABC,如图,点D在△ABC的AB边上,且∠ACD=∠A.
已知△ABC,如图,点D在△ABC的AB边上,且∠ACD=∠A.