题目内容
12.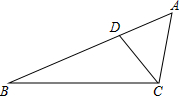 已知△ABC,如图,点D在△ABC的AB边上,且∠ACD=∠A.
已知△ABC,如图,点D在△ABC的AB边上,且∠ACD=∠A.(1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系,并说明理由.
分析 (1)利用基本作图(作已知角的平分线)作∠BDC的平分线DE;
(2)先根据角平分线的定义得到∠BDE=∠CDE,再利用三角形外角性质得∠BDC=∠A+∠ACD,加上∠ACD=∠A,则∠BDE=∠A,然后根据平行线的判定方法可判断DE∥BC.
解答 解:(1)如图,DE为所作;
(2)DE∥AC.理由如下:
∵DE平分∠BDC,
∴∠BDE=∠CDE,
而∠BDC=∠A+∠ACD,
即∠BDE+∠CDE=∠A+∠ACD,
∵∠ACD=∠A,
∴∠BDE=∠A,
∴DE∥BC.
点评 本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
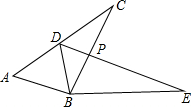 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1. 如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线上y=-$\frac{3}{4}$x上,求点B与其对应点B′间的距离.
如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线上y=-$\frac{3}{4}$x上,求点B与其对应点B′间的距离.