题目内容
18.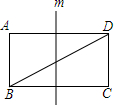 如图,直线m是矩形ABCD的一条对称轴,∠ADB=30°,点P是直线m上一点,且使得△PAB和△PAD均为等腰三角形,则满足条件的点P共有( )
如图,直线m是矩形ABCD的一条对称轴,∠ADB=30°,点P是直线m上一点,且使得△PAB和△PAD均为等腰三角形,则满足条件的点P共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据线段垂直平分线的性质可得△PAD为等腰三角形,△PAB为等腰三角形,有三种可能:AP=AB或BP=BA或PA=PB.若AP=AB,则点P在以点A为圆心,AB
为半径的圆与直线m的交点处;若BP=BA,则点P在以点B为圆心,BA为半径的圆与直线m的交点处;若PA=PB,则点P在AB的垂直平分线与直线m的交点处.
画出图象,就可解决问题.
解答 解:∵直线m是矩形ABCD的一条对称轴,点P是直线m上一点,
∴PA=PC,∠A=90°,
∴△PAD为等腰三角形.
∵∠ADB=30°,
∴∠ABD=60°.
∵△PAB为等腰三角形,
∴AP=AB或BP=BA或PA=PB.
如图所示,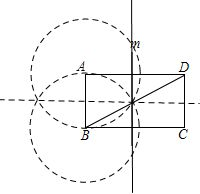
由图可知:满足条件的点P共有3个.
故选C.
点评 本题主要考查了等腰三角形的判定、线段垂直平分线的性质等知识,需要注意的是等腰△PAB并没有指明哪个是腰,需分三种情况讨论,在数满足条件的点的个数时,要考虑有没有重合的现象.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
9.已知一次函数y=x+m-3的图象与y轴的交点在x轴上方,则m需满足( )
| A. | m<3 | B. | m≤-3 | C. | m≥3 | D. | m>3 |
13.为了解决某年级学生每周做家务劳动的时间,某综合实践活动小组对该年级随机抽取的50名学生进行了调查,有关数据如下表
根据表中的数据,回答下列问题:
(1)该班学生每周做家务劳动的平均数、中位数、众数分别是多少小时?
(2)说明(1)中的三个数的意义;
(3)该校年级共有学生450名,请估计该年级学生每周做家务劳动的平均时间.
| 每周做家务的时间(小时) | 0 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 人数(人) | 2 | 2 | 6 | 8 | 12 | 13 | 4 | 3 |
(1)该班学生每周做家务劳动的平均数、中位数、众数分别是多少小时?
(2)说明(1)中的三个数的意义;
(3)该校年级共有学生450名,请估计该年级学生每周做家务劳动的平均时间.
