题目内容
17．
如图，△ABC是等边三角形，AB=6，若点D与点E分别是AB，AC的中点，则DE的长等于3．
分析 直接利用等边三角形的性质得出BC的长，再利用三角形中位线的性质得出答案．
解答 解：∵△ABC是等边三角形，AB=6，
∴BC=6，
∵点D与点E分别是AB，AC的中点，
∴DE=$\frac{1}{2}$BC=3．
故答案为：3．
点评 此题主要考查了等边三角形的性质以及三角形中位线定理，正确得出BC的长是解题关键．
练习册系列答案
相关题目
如图，在直角三角形ABC中，∠C=90°，AC=8，BC=6，设直线1⊥BC，且l从C向B平移，若CH=x，阴影部分面积为y，试求y关于x的函数关系式．
8．不等式组$\left\{\begin{array}{l}{x≥-3}\\{x＜5}\end{array}\right.$的解是（ ）
| A． | -3＜x≤5 | B． | x≥-3 | C． | -3≤x＜5 | D． | x＜5 |
甲、乙两同学从A地出发，骑自行车在同一路上行驶到B地，他们离出发地的距离s（千米）与行驶的时间t（小时） 之间的函数关系如图所示，根据图中提供的信息，有下列说法：
12．如果一个一元二次方程的根是x1=x2=2，那么这个方程可能是（ ）
| A． | （x+2）2=0 | B． | （x-2）2=0 | C． | x2=4 | D． | x2+4=0 |
2．
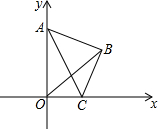如图，在平面直角坐标系中，已知AB=BC，∠ABC=90°，若点A落在y轴上，点C落在x轴上，△ABC的形状始终不变，随着点C由原点O向x轴正半轴方向运动，点A沿y轴负半轴方向运动到终点O，在此次运动过程中，线段OB的长度变化情况是（ ）
如图，在平面直角坐标系中，已知AB=BC，∠ABC=90°，若点A落在y轴上，点C落在x轴上，△ABC的形状始终不变，随着点C由原点O向x轴正半轴方向运动，点A沿y轴负半轴方向运动到终点O，在此次运动过程中，线段OB的长度变化情况是（ ）| A． | 一直增大 | B． | 一直减小 | C． | 先减小后增大 | D． | 先增大后减小 |
9．下列关于正比例函数y=3x的说法中，正确的是（ ）
| A． | 当x=3时，y=1 | B． | 它的图象是一条过原点的直线 | ||
| C． | y随x的增大而减小 | D． | 它的图象经过第二、四象限 |
6．
如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，点P是线段AB上的一动点，将△ABC绕点C按顺时针方向旋转，得到△A1B1C1，点E是线段A1C的中点，则PE长度的最小值为（ ）
如图，在Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，点P是线段AB上的一动点，将△ABC绕点C按顺时针方向旋转，得到△A1B1C1，点E是线段A1C的中点，则PE长度的最小值为（ ）| A． | $\sqrt{2}$-1 | B． | $\sqrt{3}$-1 | C． | $\sqrt{2}$+1 | D． | $\sqrt{3}$+1 |
7．
抛物线y=ax2+bx+c（a≠0）的图象如图所示，则下列说法正确的是（ ）
抛物线y=ax2+bx+c（a≠0）的图象如图所示，则下列说法正确的是（ ）| A． | a+b+c＞0 | B． | abc＞0 | C． | b2-4ac＜0 | D． | 2a+b＜0 |