题目内容
11.等边三角形的边心距为$\sqrt{3}$,则该等边三角形的边长是( )| A. | 3$\sqrt{3}$ | B. | 6 | C. | 2$\sqrt{3}$ | D. | 2 |
分析 根据题意画出图形,先根据等边三角形的性质得出∠OBD=30°,根据锐角三角函数的定义得出BD的长,由垂径定理即可得出结论.
解答  解:如图所示,
解:如图所示,
∵△ABC是等边三角形,边心距OD=$\sqrt{3}$,
∴∠OBD=30°,
∴BD=$\frac{OD}{tan30°}$=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{3}}$=3.
∵OD⊥BC,
∴BC=2BD=6.
故选B.
点评 本题考查的是正多边形和圆,熟知正三角形的性质是解答此题的关键.

练习册系列答案
相关题目
6.计算(-3)-9的结果等于( )
| A. | 6 | B. | -12 | C. | 12 | D. | -6 |
16.下列事件中,是确定性事件的是( )
| A. | 甲、乙、丙三人随意站成一排,而甲恰好站中间 | |
| B. | 从含有1个次品的10个产品中,随意抽取一个产品恰好是次品 | |
| C. | 早晨,太阳从西方升起 | |
| D. | 明天早晨八点是上班高峰期,学校门前的公路上必塞 |
1.若关于x的一元二次方程x2+(k+3)x+2=0的一个根是-1,则另一个根是( )
| A. | 1 | B. | 0 | C. | 2 | D. | -2 |
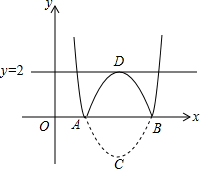 抛物线y=x2+bx+c与x轴交于点A、B,顶点为C,若将此抛物线沿x轴向上翻折,使点C落在点D处,得到如图所示图形记作图形F.
抛物线y=x2+bx+c与x轴交于点A、B,顶点为C,若将此抛物线沿x轴向上翻折,使点C落在点D处,得到如图所示图形记作图形F.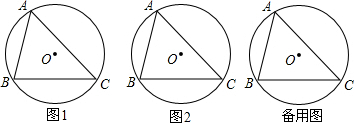
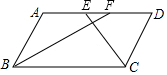 如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )
如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( )