题目内容
11．
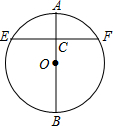如图，在⊙O中，直径AB的长度为4a，3AC=CB，过点C作EF⊥AB，交⊙O于点E，F，则EF的长度为2$\sqrt{3}$a．
分析 连接OE，根据3AC=CB，得AC=OC=$\frac{1}{2}$OA，根据勾股定理得出EF即可．
解答 
解：连接OE，
∵3AC=CB，EF⊥AB，
∴AC=OC=$\frac{1}{2}$OA，CE=CF，
∵AB=4a，
∴OA=2a，
在Rt△OCE中，OC2+EC2=OE2，
∴EC2=4a2-a2，
∴EC=$\sqrt{3}$a，
∴EF=2$\sqrt{3}$a，
故答案为2$\sqrt{3}$a．
点评 本题考查了垂径定理、勾股定理，掌握定理的内容是解题的关键．
练习册系列答案
相关题目
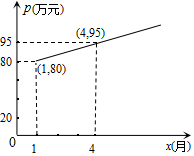在气候对人类生存压力日趋加大的今天，发展低碳经济，全面实现低碳生活成为人们的共识，某企业采用技术革新，节能减排，经分析前5个月二氧化碳排放量y（吨）与月份x（月）之间的函数关系是y=-2x+50．
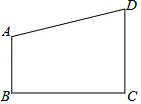在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的四边形，AB∥CD，CD⊥BC于C，且AB、BC、CD边长分别为2，4，3，则原直角三角形纸片的斜边长是4$\sqrt{5}$或10．
如图，是一个物体的展开图（单位：cm），那么这个物体的体积为250πcm3．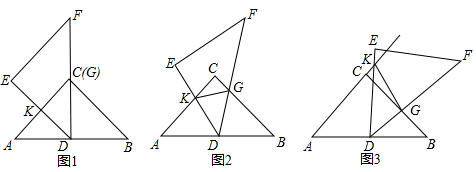
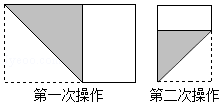长为1，宽为a的矩形纸片（$\frac{1}{2}$＜a＜1），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n此操作后，剩下的矩形为正方形，则操作终止．当n=3时，求a的值．