题目内容
1.有两个一元二次方程,M:ax2+bx+c=0;N:cx2+bx+a=0(其中a•c≠0,a≠c )则下列结论中,其中正确的是①②.(填序号)①如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
②如果5是方程M的一个根,那么$\frac{1}{5}$是方程N的一个根;
③如果方程M和方程N有一个相同的根,那么这个根必是x=1.
分析 根据判别式的意义可对①进行判断;根据一元二次方程的解的意义可对②进行判断;解方程ax2+bx+c=cx2+bx+a,即可对③进行判断.
解答 解:①如果方程M有两个不相等的实数根,那么△=b2-4ac>0,所以方程N也有两个不相等的实数根,故①正确,符合题意;
②如果5是方程M的一个根,那么25a+5b+c=0,方程两边同时除以25,得a+$\frac{1}{5}$b+$\frac{1}{25}$c=0,即$\frac{1}{25}$c+$\frac{1}{5}$b+a=0,所以$\frac{1}{5}$是方程N的一个根,故②正确,符合题意;
③如果方程M和方程N有一个相同的根,那么ax2+bx+c=cx2+bx+a,解得x=±1,故③错误,不符合题意;
故答案为①②.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.上面的结论反过来也成立.同时考查了一元二次方程的解.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
11.已知二元一次方程组$\left\{\begin{array}{l}{5x+4y=5}&{①}\\{3x+2y=9}&{②}\end{array}\right.$下列说法正确的是( )
| A. | 适合方程②的x,y的值是方程组的解 | |
| B. | 适合方程①的x,y的值是方程组的解 | |
| C. | 同时适合方程①和②的x,y的值是方程组的解 | |
| D. | 同时适合方程①和②的x,y的值不一定是方程组的解 |
6. 如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF=( )
如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF=( )
 如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF=( )
如图,AB∥EF∥CD,∠ABC=46°,∠BCE=20°,则∠CEF=( )| A. | 144° | B. | 154° | C. | 164° | D. | 160° |
 如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是垂线段最短.
如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是垂线段最短.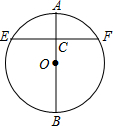 如图,在⊙O中,直径AB的长度为4a,3AC=CB,过点C作EF⊥AB,交⊙O于点E,F,则EF的长度为2$\sqrt{3}$a.
如图,在⊙O中,直径AB的长度为4a,3AC=CB,过点C作EF⊥AB,交⊙O于点E,F,则EF的长度为2$\sqrt{3}$a.