题目内容
18.计算:(1)($\frac{x}{x+1}$-$\frac{3x}{x-1}$)÷$\frac{x}{{x}^{2}-1}$
(2)(1+$\frac{2b}{a-b}$)2•(1-$\frac{2b}{a+b}$)2.
分析 根据分式的混合运算顺序:先算乘方,再算乘除,最后算加减,有括号的先算括号里的进行计算.
解答 解:(1)($\frac{x}{x+1}$-$\frac{3x}{x-1}$)÷$\frac{x}{{x}^{2}-1}$
=$\frac{x(x-1)-3x(x+1)}{{x}^{2}-1}•\frac{{x}^{2}-1}{x}$
=x-1-3(x+1)
=-2x-4;
(2)(1+$\frac{2b}{a-b}$)2•(1-$\frac{2b}{a+b}$)2
=$(\frac{a-b+2b}{a-b})^{2}•(\frac{a+b-2b}{a+b})^{2}$
=$\frac{(a+b)^{2}(a-b)^{2}}{(a-b)^{2}(a+b)^{2}}$
=1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
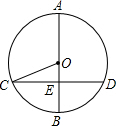 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=26,CD=24,则$\frac{OE}{BE}$=$\frac{5}{8}$.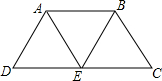 四边形ABCD中,DC∥AB,DC=2AB,E为DC的中点,连结AE、EB
四边形ABCD中,DC∥AB,DC=2AB,E为DC的中点,连结AE、EB