题目内容
4.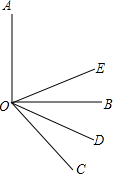 如图,已知OE是∠AOC的平分线,OD是∠BOC的平分线,若∠AOB=90°,求∠DOE的度数.
如图,已知OE是∠AOC的平分线,OD是∠BOC的平分线,若∠AOB=90°,求∠DOE的度数.
分析 根据角平分线的定义以及角的和、差即可得到∠EOD=∠EOC-∠COD=$\frac{1}{2}$∠AOC-$\frac{1}{2}$BOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB,从而求解.
解答 解:∵OE是∠AOC的平分线,OD是∠BOC的平分线,
∴∠EOC=$\frac{1}{2}$∠AOC,∠COD=$\frac{1}{2}$∠BOC,
∴∠EOD=∠EOC-∠COD=$\frac{1}{2}$∠AOC-$\frac{1}{2}$BOC=$\frac{1}{2}$(∠AOC-∠BOC)=$\frac{1}{2}$∠AOB=45°.
点评 本题考查了角度的计算,角平分线的定义,证明的∠EOD=$\frac{1}{2}$∠AOB是关键.

练习册系列答案
相关题目
19.下列说法中错误的是( )
| A. | 如果a<b,那么a-c<b-c | B. | 如果a>b,c>0,那么ac>bc | ||
| C. | 如果m<n,p<0,那么$\frac{m}{p}$>$\frac{n}{p}$ | D. | 如果x>y,z<0,那么xz>yz |