题目内容
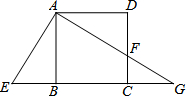 如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=
如图,四边形ABCD是正方形,点E在CB的延长线上,连结AE,将△ABE绕点A逆时针旋转90°,得到△ADF,点E落在DC上的点F处,AF的延长线交BC延长线于点G.若AB=3,AE=| 13 |
| A、1.5 | B、1.6 |
| C、1.8 | D、2 |
考点:旋转的性质,勾股定理,相似三角形的判定与性质
专题:计算题
分析:先根据正方形的性质得AB=AD=CD=3,再根据旋转的性质得AF=AE=
,则可根据勾股定理计算出DF=2,所以CF=CD-DF=1,然后证明△CGF∽△DAF,再利用相似比可计算出CG.
| 13 |
解答:解:∵四边形ABCD是正方形,
∴AB=AD=CD=3,
∵△ABE绕点A逆时针旋转90°,得到△ADF,
∴AF=AE=
,
在Rt△ADF中,∵AD=3,AF=
,
∴DF=
=2,
∴CF=CD-DF=3-2=1,
∵AD∥CG,
∴△CGF∽△DAF,
∴
=
,即
=
,
∴CGF=1.5.
故选A.
∴AB=AD=CD=3,
∵△ABE绕点A逆时针旋转90°,得到△ADF,
∴AF=AE=
| 13 |
在Rt△ADF中,∵AD=3,AF=
| 13 |
∴DF=
| AF2-AD2 |
∴CF=CD-DF=3-2=1,
∵AD∥CG,
∴△CGF∽△DAF,
∴
| CG |
| AD |
| CF |
| DF |
| CG |
| 3 |
| 1 |
| 2 |
∴CGF=1.5.
故选A.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
“染色体”是人类“生命之书”中最长也是最后被破解的一章,据报道,第一号染色体中共有2.23亿个碱基对,2.23亿用科学记数法可表示为( )
| A、2.23×106 |
| B、2.23×108 |
| C、2.23×109 |
| D、223×106 |
武汉市希望中学开展以“我最喜欢的职业”为主题的调查活动,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制的不完整的统计图,则下列说法中,不正确的是( )
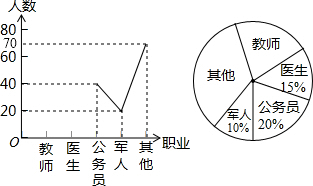

| A、被调查的学生有200人 |
| B、扇形图中公务员部分所对应的圆心角为72° |
| C、被调查的学生中喜欢其他职业的占40% |
| D、被调查的学生中喜欢教师职业的有40人 |
 【问题情镜】
【问题情镜】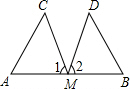 已知:如图,M是AB的中点,∠1=∠2,MC=MD.求证:△ACM≌△BDM.
已知:如图,M是AB的中点,∠1=∠2,MC=MD.求证:△ACM≌△BDM.