题目内容
12.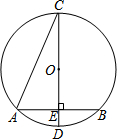 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=6cm,则⊙O半径为6cm.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=15°,AB=6cm,则⊙O半径为6cm.
分析 连接OA,由圆周角定理得出∠AOE=2∠C=30°,由垂径定理得出AE=BE=$\frac{1}{2}$AB=3cm,得出OA=2OE=6cm即可.
解答 解:连接OA,如图所示
则∠AOE=2∠C=30°,
∵AB⊥CD,
∴AE=BE=$\frac{1}{2}$AB=3cm,
∴OA=2OE=6cm,
即⊙O半径为6cm;
故答案为:6.
点评 本题考查了垂径定理、圆周角定理以及含30°角的直角三角形的性质;熟练掌握圆周角定理,由垂径定理求出AE是解决问题的关键.

练习册系列答案
相关题目
13.电子比荷是自然科学中的重要常数,其数值约为1760亿,若将1760亿用科学记数法表示为1.76×10n,则n的值是( )
| A. | 10 | B. | 11 | C. | 12 | D. | -11 |
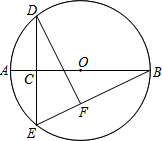 已知:⊙O的半径为5,点C在直径AB上,过点C作⊙O的弦DE⊥AB,过点D作直线 EB的垂线DF,垂足为点F,设AC=x,EF=y.
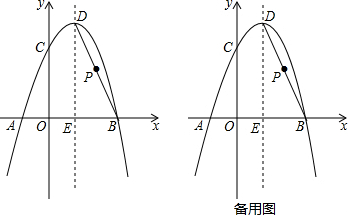
已知:⊙O的半径为5,点C在直径AB上,过点C作⊙O的弦DE⊥AB,过点D作直线 EB的垂线DF,垂足为点F,设AC=x,EF=y. 当某一面积S关于某一线段x是一次函数时,则称S是关于x的奇特面积.如图,∠BAC=45°,点D在AC边上,且DA=2.点P,Q同时从D点出发,分别沿射线DC、射线DA运动,P点的运行速度是Q点的$\sqrt{2}$倍,当点Q到达A时,点P,Q同时停止运动.过点Q作AC的垂线段QR,使QR=PQ,连接PR.设QD=x,△PQR和∠BAC重叠部分的面积为S,请问S是否存在关于x的奇特面积?若存在,求奇特面积S关于x的函数关系式;若不存在,请说明理由.
当某一面积S关于某一线段x是一次函数时,则称S是关于x的奇特面积.如图,∠BAC=45°,点D在AC边上,且DA=2.点P,Q同时从D点出发,分别沿射线DC、射线DA运动,P点的运行速度是Q点的$\sqrt{2}$倍,当点Q到达A时,点P,Q同时停止运动.过点Q作AC的垂线段QR,使QR=PQ,连接PR.设QD=x,△PQR和∠BAC重叠部分的面积为S,请问S是否存在关于x的奇特面积?若存在,求奇特面积S关于x的函数关系式;若不存在,请说明理由.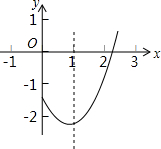 在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0.
在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是-1<x2<0.