题目内容
 如图,在菱形ABCD中,∠A=130°,E、F分别是边AB、AD的中点,EP⊥DC的延长线于点P,则∠FPD=
如图,在菱形ABCD中,∠A=130°,E、F分别是边AB、AD的中点,EP⊥DC的延长线于点P,则∠FPD=考点:菱形的性质
专题:
分析:延长PF交BA的延长线于G,连接EF,根据菱形的性质先求得AE=AF,根据等边对等角得出∠AEF=∠AFE=25°,然后根据三角形相似求得F是PG的中点,根据直角三角形斜边的中线的性质得出EF=FG,从而得出∠AEF=∠EGF=25°,进而得出∠FPD=25°.
解答: 解:延长PF交BA的延长线于G,连接EF,
解:延长PF交BA的延长线于G,连接EF,
∵四边形ABCD是菱形,
∴AB=AD,
∵E、F分别是边AB、AD的中点,
∴AE=AF,
∴∠AEF=∠AFE,
∵∠A=130°,
∴∠AEF=25°,
∵PD∥BG,
∴∠FPD=∠FGE,
∵∠PFD=∠AFG,
∴△PFD∽△GFA,
∴
=
,
∵AF=FD,
∴GF=PF,
∵PE⊥DC,
∴PE⊥BG,
∴EF=FG,
∴∠AEF=∠EGF=25°,
∴∠FPD=25°.
故答案为25°.
 解:延长PF交BA的延长线于G,连接EF,
解:延长PF交BA的延长线于G,连接EF,∵四边形ABCD是菱形,
∴AB=AD,
∵E、F分别是边AB、AD的中点,
∴AE=AF,
∴∠AEF=∠AFE,
∵∠A=130°,
∴∠AEF=25°,
∵PD∥BG,
∴∠FPD=∠FGE,
∵∠PFD=∠AFG,
∴△PFD∽△GFA,
∴
| AF |
| FD |
| GF |
| PF |
∵AF=FD,
∴GF=PF,
∵PE⊥DC,
∴PE⊥BG,
∴EF=FG,
∴∠AEF=∠EGF=25°,
∴∠FPD=25°.
故答案为25°.
点评:本题考查了菱形的性质,等腰三角形的判定及其性质,三角形相似的判定和性质,平行线的性质等,作出辅助线构建直角三角形是本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.求证:
如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.求证: 如图,四边形ABCD中,要使AB∥CD,可添加哪些条件?(不添加辅助线,至少写出3个)
如图,四边形ABCD中,要使AB∥CD,可添加哪些条件?(不添加辅助线,至少写出3个)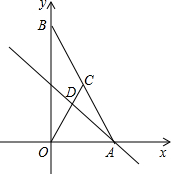 如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组
如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组 如图,AB、ED分别垂直于BD,点B、D是垂足,且AB=CD,AC=CE.
如图,AB、ED分别垂直于BD,点B、D是垂足,且AB=CD,AC=CE. 如图,已知BC>AB,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°.
如图,已知BC>AB,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°. 如图,小河CD边有两个村庄A村、B村,现要在河边建一自来水厂E为A村与B村供水,自来水厂建在什么地方到A村、B村的距离和最小?请在下图中找出点E的位置.(保留作图痕迹,不写作法)
如图,小河CD边有两个村庄A村、B村,现要在河边建一自来水厂E为A村与B村供水,自来水厂建在什么地方到A村、B村的距离和最小?请在下图中找出点E的位置.(保留作图痕迹,不写作法)