题目内容
19．
用一块直径为4米的圆桌布平铺在对角线长为8米的正六边形桌面上（如图），若四周下垂的最大长度相等，则这个最大长度x为2-$\sqrt{3}$米．
分析 画出平面图，连接OA，作OM⊥AB，垂足为N，交⊙O于M，由正六边形的性质得出OA、AM，MN=x，求出OM的长，即可得出结果．
解答 解：平面图如图所示
连接OA，作OM⊥AB，垂足为N，交⊙O于M，
则OA=2，MN=x，∠AOM=30°，
∴AM=$\frac{1}{2}$OA=1，
∴OM=$\sqrt{3}$AM=$\sqrt{3}$，
∴x=ON-OM=2-$\sqrt{3}$（米）．
故答案为：2-$\sqrt{3}$．
点评 本题考查了正多边形和圆的位置关系、正六边形的性质；熟练掌握正六边形的性质，画出图形，由正六边形的性质求出OM是解决问题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
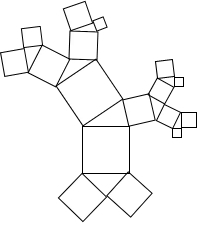如图，美丽的珊瑚礁图案中，所有的四边形都是正方形，所有的三角形都是直角三角形．所有正方形（包括最大的正方形）的面积之和为500cm2，最大的正方形边长为10．
已知一个由50个偶数排成的数阵，请你观察框内的四个数之间的关系并解答下列问题：在数阵中任意作一个类似图中的框．
如图，在?ABCD中，E为BC中点，DE、AC交于F点，则$\frac{EF}{ED}$=$\frac{1}{3}$．
已知：如图，把长方形纸片ABCD沿EF折叠后，点D与点B重合，点C落在点C'的位置上，若∠1=60°，AE=1．
为纪念爱国诗人屈原，我市在俯南河隆重举行了一次龙舟比赛，如图是甲、乙两支龙舟队在比赛时的路程s（米）与时间t（分钟）之间的图象，请你根据图象回答下列问题：
如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点A1．