题目内容
11. 已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.
已知:如图,把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C'的位置上,若∠1=60°,AE=1.(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的边AD的长.
分析 (1)根据AD∥BC,∠1与∠2是内错角,因而就可以求得∠2,根据图形的折叠的定义,可以得到∠4=∠2,进而可以求得∠3的度数;
(2)已知AE=1,在Rt△ABE中,根据三角函数就可以求出AB、BE的长,BE=DE,则可以求出AD的长.
解答  解:(1)∵AD∥BC,
解:(1)∵AD∥BC,
∴∠2=∠1=60°;
又∵∠4=∠2=60°,
∴∠3=180°-60°-60°=60°.
(2)在直角△ABE中,由(1)知∠3=60°,
∴∠5=90°-60°=30°;
∴BE=2AE=2,
∴AB=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$;
∴AD=AE+DE=AE+BE=1+2=3.
点评 此题考查了矩形的性质,折叠的性质以及直角三角形的性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,将△ABC的∠A沿DE折叠,探索∠1,∠2,∠A之间的数量关系2∠A=∠1-∠2.
如图,将△ABC的∠A沿DE折叠,探索∠1,∠2,∠A之间的数量关系2∠A=∠1-∠2. 用一块直径为4米的圆桌布平铺在对角线长为8米的正六边形桌面上(如图),若四周下垂的最大长度相等,则这个最大长度x为2-$\sqrt{3}$米.
用一块直径为4米的圆桌布平铺在对角线长为8米的正六边形桌面上(如图),若四周下垂的最大长度相等,则这个最大长度x为2-$\sqrt{3}$米.
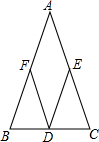 已知:如图,等腰△ABC中,AB=AC,D是BC的中点,DE∥AB,DF∥AC,求证:四边形AFDE是菱形.
已知:如图,等腰△ABC中,AB=AC,D是BC的中点,DE∥AB,DF∥AC,求证:四边形AFDE是菱形. 如图,在平面直角坐标系中,点O为坐标原点,△OAB的顶点B在x轴负半轴上,OA=OB=5,tan∠AOB=$\frac{3}{4}$,点P与点A关于y轴对称,点P在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,点O为坐标原点,△OAB的顶点B在x轴负半轴上,OA=OB=5,tan∠AOB=$\frac{3}{4}$,点P与点A关于y轴对称,点P在反比例函数y=$\frac{k}{x}$的图象上. 如图,按要求画出图形.
如图,按要求画出图形.