题目内容
5.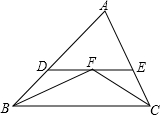 如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,求证:
如图所示,∠ABC和∠ACB的平分线相交于F,过F作DE∥BC,交AB于D,交AC于E,求证:(1)DB=DF;
(2)DB+EC=DE.
分析 (1)利用角平分线性质可得两组角相等,再结合平行线的性质,可证出∠DBF=∠DFB,那么利用等角对等边可得线段的相等;
(2)利用角平分线性质可得两组角相等,再结合平行线的性质,可证出∠DBF=∠DFB,∠ECF=∠EFC,那么利用等角对等边可得线段的相等,再利用等量代换可证.
解答 证明:(1)∵BF是∠ABC的角平分线,
∴∠DBF=∠FBC,
又∵DE∥BC,
∴∠BFD=∠CBF,
∴∠DBF=∠DFB,
∴BD=DF;
(2)∵BF、CF是∠ABC、∠ACB的角平分线,
∴∠DBF=∠FBC,∠ECF=∠BCF.
又∵DE∥BC,
∴∠BFD=∠CBF,∠BCF=∠EFC.
∴∠DBF=∠DFB,∠ECF=∠EFC.
∴BD=DF,CE=EF.
∴DE=DF+EF=BD+CE.
点评 本题考查了角平分线性质、平行线性质、以及等角对等边的性质等.进行线段的等量代换是正确解答本题的关键.

练习册系列答案
相关题目
16.汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值是( )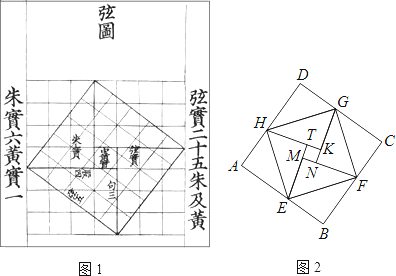

| A. | $\frac{11}{3}$ | B. | $\frac{10}{3}$ | C. | 3 | D. | $\frac{8}{3}$ |
17.下列关于正六边形的说法错误的是( )
| A. | 边都相等 | B. | 对角线都相等 | C. | 内角都相等 | D. | 外角都相等 |
14.$\sqrt{5}$的相反数是( )
| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | -$\frac{1}{{\sqrt{5}}}$ | D. | $\frac{1}{{\sqrt{5}}}$ |
 如图,△ABC经过旋转变换得到△AB′C′,若∠CAC′=35°,则∠BAB′=35度.
如图,△ABC经过旋转变换得到△AB′C′,若∠CAC′=35°,则∠BAB′=35度.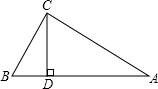 如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长.
如图,△ABC中,∠ACB=90°,CD是高,∠A=30°,AB=5,求BD的长. 已知:AB=CD,AE⊥BC于E,DF⊥BC于F,且CE=BF,求证:∠A=∠D.
已知:AB=CD,AE⊥BC于E,DF⊥BC于F,且CE=BF,求证:∠A=∠D.