题目内容

已知等腰三角形的一个外角是135°，则它顶角的度数为
 
．
考点：等腰三角形的性质
专题：
分析：先求出与这个外角相邻的内角是45°，再分这个内角是底角和顶角两种情况讨论．
解答：解：与这个外角相邻的内角为：180°-135°=45°．
分两种情况：
（1）当45°角为底角时，顶角为180°-45°×2=90°；
（2）当45°角为顶角时，顶角为45°．
故顶角的度数是90°或45°．
故答案为：90°或45°．
点评：本题考查了等腰三角形的性质；若题目中没有明确顶角或底角的度数，做题时要注意分情况进行讨论，这是十分重要的，也是解答问题的关键．
练习册系列答案
相关题目
在一个边长为a（单位：cm）的正方形ABCD中．
（1）如图1，如果N是AD中点，F为AB中点，连接DF，CN．
①求证：DF=CN；
②连接AC．则DH：HE：EF=
 
．（直接写出结果）
（2）如图2，如果点E、M分别是线段AC、CD上的动点，假设点E从点A出发，以
2
cm/s速度沿AC向点C运动，同时点M从点C出发，以1cm/s的速度沿CD向点D运动，运动时间为t（t＞0），连结DE并延长，交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．求证：当点F是边AB中点时，DM=2CM．
如果n边形的内角和等于外角和的3倍，那么n的值是（　　）
A、5B、6C、7D、8
用“＜”、“＞”或“=”填空：
3
2
3
 
12
．
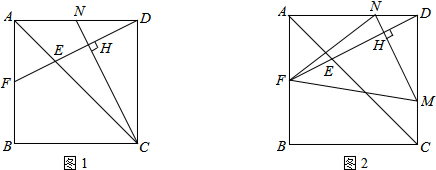
如图，点F，E分别是AB，AC上的点，连接FE交BC的延长线于点D，AE•CE=EF•ED．找出图中所有相似的三角形，并证明．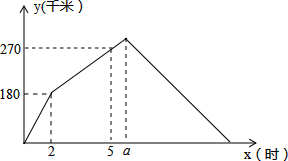
甲、乙两车都从同一地点沿同一路线驶向同一目的地，甲车先行，一段时间后，乙车开始行驶，甲车到达目的地后，乙车走完了全程的
4
9
，下图反应的是从甲车开始行驶到乙车到达目的地整个过程中两车之间的距离与时间的函数关系图象，则a=
 
．
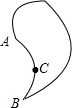右图中，半圆弧
ACB
直径AB为4.5厘米，以A点为圆心，将半圆弧
ACB
逆时针转动100度，得到右图所示的图形，那么这个图形的周长等于
 
厘米（取π=3.14）
如图，点E，F分别是矩形ABCD的边AD，BC的三等分点（距D、C近），若矩形ABFE与矩形ABCD相似，则矩形ABCD的AD：AB是
 
．
已知：如图，在?ABCD中，AC、BD相交于点O，点E、F分别在OB、OD上，且OE=OF．求证：四边形AECF是平行四边形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网